/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 27 kwietnia 2019 Czas pracy: 170 minut
Zadania zamknięte
Liczba 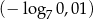 jest mniejsza od liczby
jest mniejsza od liczby 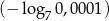 o
o
A) 100% B) 25% C) 50% D) 10%
Wartość wyrażenia 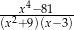 dla
dla 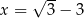 jest równa
jest równa
A) 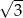 B)
B) 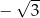 C) 3 D)
C) 3 D) 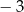
Dane są liczby 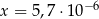 oraz
oraz 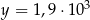 . Wtedy iloraz
. Wtedy iloraz 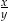 jest równy
jest równy
A) 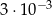 B)
B) 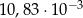 C)
C) 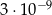 D)
D) 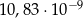
Czas trwania zabiegu rehabilitacyjnego wydłużono o 35% do 108 minut. Ile początkowo miał trwać ten zabieg?
A) 80 minut B) 90 minut C) 60 minut D) 70 minut
Zbiorem rozwiązań nierówności 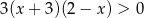 jest zbiór zaznaczony na osi liczbowej:
jest zbiór zaznaczony na osi liczbowej:

Równanie 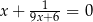
A) ma dokładnie dwa rozwiązania rzeczywiste.
B) ma dokładnie trzy rozwiązania rzeczywiste.
C) ma dokładnie jedno rozwiązanie rzeczywiste.
D) nie ma rozwiązań.
Jeśli wykres funkcji kwadratowej 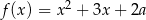 jest styczny do prostej
jest styczny do prostej 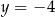 , to
, to
A) 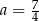 B)
B) 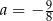 C)
C) 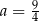 D)
D) 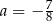
Wykres funkcji liniowej 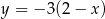 przecina prostą
przecina prostą 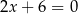 w punkcie
w punkcie
A) 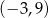 B)
B) 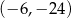 C)
C) 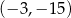 D)
D) 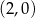
Dane są funkcje 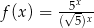 oraz
oraz 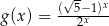 , określone dla wszystkich liczb rzeczywistych
, określone dla wszystkich liczb rzeczywistych  . Punkt wspólny wykresów funkcji
. Punkt wspólny wykresów funkcji 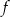 i
i 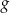
A) nie istnieje B) ma współrzędne 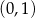
C) ma współrzędne 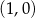 D) ma współrzędne
D) ma współrzędne 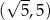
Zbiorem wartości funkcji 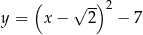 określonej w przedziale
określonej w przedziale 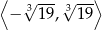 jest
jest
A) 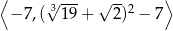 B)
B) 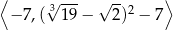
C) 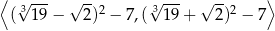 D)
D) 
Funkcja kwadratowa jest określona wzorem  . Liczby
. Liczby  są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji  . Zatem
. Zatem
A) 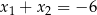 B)
B) 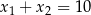 C)
C) 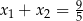 D)
D) 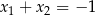
W ciągu arytmetycznym 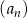 , określonym dla
, określonym dla 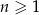 , spełniony jest warunek
, spełniony jest warunek 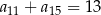 . Wtedy
. Wtedy
A) 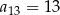 B)
B) 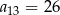 C)
C) 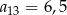 D)
D) 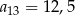
W rosnącym ciągu geometrycznym 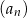 , określonym dla
, określonym dla 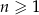 , spełniony jest warunek
, spełniony jest warunek 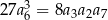 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 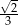 B)
B) 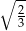 C)
C) 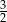 D)
D) 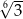
Układ równań 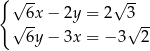
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C)ma nieskończenie wiele rozwiązań. D) ma dokładnie dwa rozwiązania.
Kąt  jest ostry i
jest ostry i 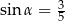 . Wtedy
. Wtedy
A) 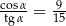 B)
B) 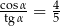 C)
C) 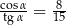 D)
D) 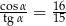
Punkty 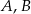 i
i 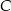 leżą na okręgu o środku
leżą na okręgu o środku 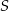 (zobacz rysunek).
(zobacz rysunek).
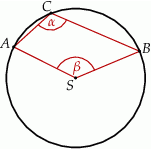
Miary  i
i 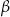 zaznaczonych kątów
zaznaczonych kątów 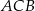 i
i 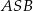 spełniają warunek
spełniają warunek 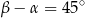 . Wynika stąd, że
. Wynika stąd, że
A) 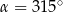 B)
B) 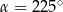 C)
C) 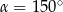 D)
D) 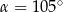
Podstawa trójkąta równoramiennego 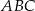 ma długość 19. Na ramionach
ma długość 19. Na ramionach 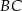 i
i 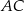 wybrano punkty
wybrano punkty 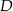 i
i 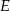 odpowiednio tak, że
odpowiednio tak, że 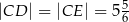 oraz
oraz 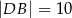 .
.
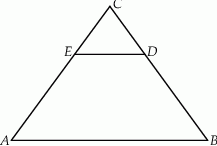
Odległość między prostymi 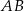 i
i 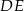 jest równa
jest równa
A) 5 B) 8 C) 10 D) 12
Okrąg o środku 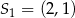 i promieniu
i promieniu  oraz okrąg o środku
oraz okrąg o środku 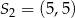 i promieniu 6 są styczne wewnętrznie. Wtedy
i promieniu 6 są styczne wewnętrznie. Wtedy
A) 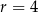 B)
B) 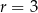 C)
C) 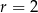 D)
D) 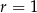
Pole trójkąta o bokach długości 8 oraz 15 i kącie między nimi o mierze 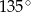 jest równe
jest równe
A) 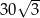 B)
B) 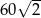 C)
C) 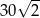 D)
D) 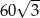
Podstawą ostrosłupa jest równoramienny trójkąt prostokątny 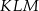 o przeciwprostokątnej długości
o przeciwprostokątnej długości 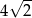 . Wysokością tego ostrosłupa jest krawędź
. Wysokością tego ostrosłupa jest krawędź 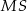 o długości 4 (zobacz rysunek).
o długości 4 (zobacz rysunek).
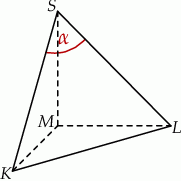
Kąt  , jaki tworzą krawędzie
, jaki tworzą krawędzie 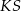 i
i 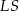 , spełnia warunek
, spełnia warunek
A) 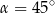 B)
B) 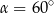 C)
C) 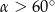 D)
D) 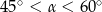
Stożek o średnicy podstawy 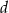 i kula o promieniu
i kula o promieniu 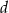 mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
A) 32 B) 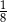 C)
C) 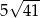 D) 4
D) 4
Punkt 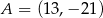 i środek
i środek 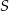 odcinka
odcinka 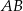 są położone symetrycznie względem początku układu współrzędnych. Zatem punkt
są położone symetrycznie względem początku układu współrzędnych. Zatem punkt 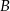 ma współrzędne
ma współrzędne
A) 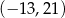 B)
B) 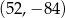 C)
C) 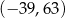 D)
D) 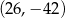
Punkty 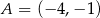 i
i 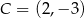 są wierzchołkami rombu
są wierzchołkami rombu 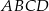 . Wierzchołki
. Wierzchołki 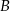 i
i 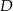 tego rombu są zawarte w prostej o równaniu
tego rombu są zawarte w prostej o równaniu 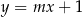 . Zatem
. Zatem
A) 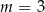 B)
B) 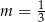 C)
C) 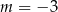 D)
D) 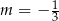
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2019 i podzielnych przez 4?
A) 256 B) 257 C) 255 D) 128
W tabeli przedstawiono procentowy podział uczestników obozu ze względu na wiek.
| Wiek uczestnika | Liczba uczestników |
| 10 lat | 20% |
| 12 lat | 40% |
| 14 lat | 25% |
| 16 lat | 15% |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Mediana wieku uczestników obozu jest równa
A) 12 lat B) 11 lat C) 10 lat D) 13 lat
Zadania otwarte
Rozwiąż nierówność 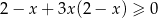 .
.
Rozwiąż równanie 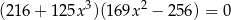 .
.
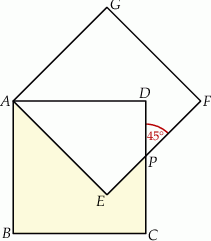
Dwa kwadraty 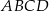 i
i 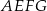 o boku długości 2 nałożono na siebie tak jak na rysunku poniżej. Oblicz pole pięciokąta
o boku długości 2 nałożono na siebie tak jak na rysunku poniżej. Oblicz pole pięciokąta 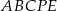 .
.
Punkty 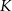 i
i 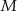 oraz
oraz 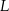 i
i 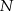 dzielą odpowiednio boki
dzielą odpowiednio boki 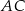 i
i 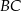 trójkąta
trójkąta 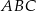 w stosunku
w stosunku 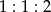 (zobacz rysunek). Odcinki
(zobacz rysunek). Odcinki 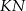 i
i 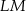 przecinają się w punkcie
przecinają się w punkcie 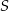 .
.
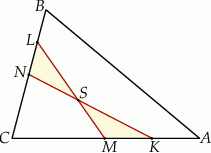
Uzasadnij, że pola trójkątów 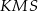 i
i 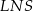 są równe.
są równe.
Udowodnij, że dla dowolnych liczb dodatnich 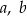 prawdziwa jest nierówność
prawdziwa jest nierówność
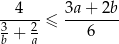
Rzucamy pięć razy symetryczną monetą. Po przeprowadzonym doświadczeniu zapisujemy liczbę uzyskanych orłów (od 0 do 5) i liczbę uzyskanych reszek (również od 0 do 5). Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tych pięciu rzutach liczba uzyskanych orłów będzie mniejsza niż liczba uzyskanych reszek.
Siódmy wyraz ciągu geometrycznego 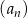 , określonego dla
, określonego dla 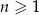 , jest równy 6, a suma jego sześciu początkowych wyrazów jest równa 756. Iloraz
, jest równy 6, a suma jego sześciu początkowych wyrazów jest równa 756. Iloraz 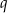 tego ciągu spełnia warunek:
tego ciągu spełnia warunek: 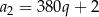 . Oblicz pierwszy wyraz oraz iloraz tego ciągu.
. Oblicz pierwszy wyraz oraz iloraz tego ciągu.
W układzie współrzędnych punkty 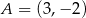 i
i 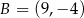 są wierzchołkami trójkąta
są wierzchołkami trójkąta 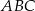 . Wierzchołek
. Wierzchołek 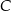 leży na prostej o równaniu
leży na prostej o równaniu 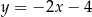 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 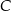 , dla którego kąt
, dla którego kąt 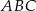 jest prosty.
jest prosty.
Dany jest ostrosłup prawidłowy czworokątny o wysokości 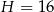 . Suma długości wszystkich jego krawędzi jest równa
. Suma długości wszystkich jego krawędzi jest równa 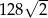 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.

