/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 11 marca 2023 Czas pracy: 180 minut
Wyznacz wartość parametru 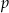 , dla którego
, dla którego
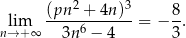
Oblicz, ile jest liczb dwunastocyfrowych takich, że suma cyfr w każdej z tych liczb jest równa 15 i żadna cyfra nie jest zerem.
Funkcja 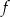 jest określona wzorem
jest określona wzorem 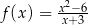 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 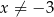 . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 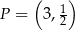 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 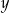 takich, że
takich, że 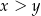 , spełniona jest nierówność
, spełniona jest nierówność
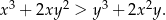
Liczby ze zbioru 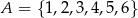 ustawiamy w losowy sposób w sześcioelementowy ciąg, przy czym każda liczba ze zbioru
ustawiamy w losowy sposób w sześcioelementowy ciąg, przy czym każda liczba ze zbioru 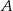 jest dokładnie jednym wyrazem tego ciągu. Oblicz prawdopodobieństwo tego, że iloczyn każdych dwóch sąsiednich wyrazów tego ciągu jest liczbą parzystą jeżeli wiadomo, że pierwszy wyraz tego ciągu jest liczbą nieparzystą.
jest dokładnie jednym wyrazem tego ciągu. Oblicz prawdopodobieństwo tego, że iloczyn każdych dwóch sąsiednich wyrazów tego ciągu jest liczbą parzystą jeżeli wiadomo, że pierwszy wyraz tego ciągu jest liczbą nieparzystą.
Dany jest nieskończony ciąg geometryczny 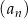 określony dla
określony dla 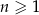 , w którym
, w którym 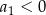 . Suma
. Suma 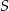 wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność
wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność 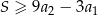 . Wykaż, ze
. Wykaż, ze 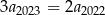 .
.
Informacja do zadań 7.1 i 7.2
Na obrzeżach miasta znajduje się jezioro, na którym postanowiono stworzyć tor regatowy. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej jeziora w kartezjańskim układzie współrzędnych 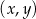 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 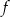 oraz
oraz 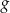 (zobacz rysunek).
(zobacz rysunek).
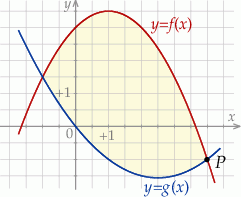
Funkcje 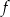 oraz
oraz 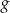 są określone wzorami
są określone wzorami 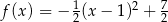 oraz
oraz 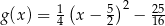 . Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt
. Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt 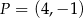 .
.
Niech 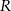 będzie punktem leżącym na wykresie funkcji
będzie punktem leżącym na wykresie funkcji 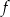 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 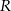 od punktu
od punktu 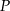 wyraża się wzorem
wyraża się wzorem
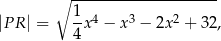
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 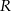 .
.
Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu 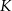 , w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca
, w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca 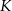 toru od początku
toru od początku 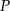 ) była możliwie największa. Oblicz długość najdłuższego toru.
) była możliwie największa. Oblicz długość najdłuższego toru.
Przy rozwiązywaniu zadania możesz skorzystać z tego, że odległość dowolnego punktu 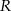 leżącego na wykresie funkcji
leżącego na wykresie funkcji 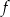 od punktu
od punktu 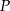 wyraża się wzorem
wyraża się wzorem
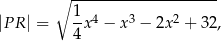
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 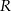 .
.
Wykaż, że
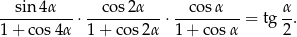
Wyznacz dziedzinę tej tożsamości.
Rozwiąż nierówność
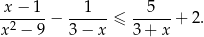
Dany jest graniastosłup prawidłowy sześciokątny o podstawie 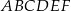 i polu powierzchni bocznej równym
i polu powierzchni bocznej równym 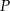 . Kąt między przekątnymi ścian bocznych wychodzącymi z wierzchołka
. Kąt między przekątnymi ścian bocznych wychodzącymi z wierzchołka 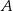 ma miarę
ma miarę 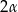 . Objętość tego graniastosłupa jest równa
. Objętość tego graniastosłupa jest równa
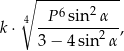
gdzie 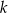 jest stałym współczynnikiem liczbowym. Oblicz współczynnik
jest stałym współczynnikiem liczbowym. Oblicz współczynnik 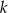 .
.
Przekątne kwadratu 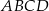 przecinają się w punkcie
przecinają się w punkcie 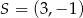 , a jeden z jego boków jest zawarty w prostej
, a jeden z jego boków jest zawarty w prostej 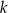 o równaniu
o równaniu 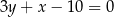 . Wyznacz współrzędne wierzchołków kwadratu
. Wyznacz współrzędne wierzchołków kwadratu 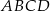 .
.
Na okręgu o średnicy 8 opisano trapez prostokątny, w którym jedna z podstaw ma długość 15. Oblicz pole tego trapezu.

