/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 17 kwietnia 2021 Czas pracy: 170 minut
Zadania zamknięte
Liczba 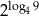 jest równa
jest równa
A) 3 B) 24 C) 9 D) 81
Liczbę 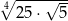 można zapisać w postaci
można zapisać w postaci
A) 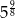 B)
B) 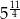 C)
C) 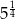 D)
D) 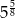
Liczba 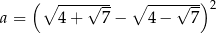 jest równa
jest równa
A) 2 B) 5 C) 8 D) 14
Cenę  pewnego towaru obniżono o 36% i otrzymano cenę
pewnego towaru obniżono o 36% i otrzymano cenę 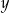 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 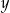 należy podnieść o
należy podnieść o
A) o 64% B) o 60% C) o 36% D) o 56,25%
Liczba 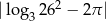 jest równa
jest równa
A) 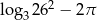 B)
B) 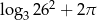 C)
C) 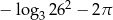 D)
D) 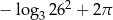
Liczba przeciwna do podwojonej odwrotności liczby  jest równa
jest równa
A) 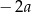 B)
B) 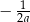 C)
C) 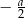 D)
D) 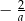
Funkcja 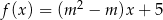 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 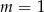 B)
B) 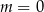 C)
C) 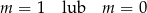 D)
D) 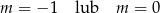
Liczba 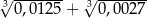 jest równa
jest równa
A) 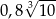 B) 0,8 C)
B) 0,8 C) 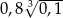 D) 0,08
D) 0,08
Zbiorem rozwiązań nierówności 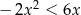 jest
jest
A) 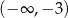 B)
B) 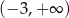 C)
C) 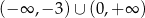 D)
D) 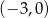
Równanie 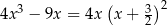 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma dokładnie trzy rozwiązania.
Na rysunku poniżej przedstawiono fragment wykresu funkcji kwadratowej 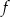 określonej wzorem
określonej wzorem 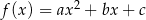 .
.
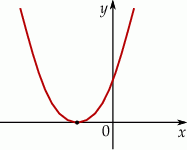
Stąd wynika, że:
A) 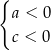 B)
B) 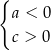 C)
C) 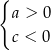 D)
D) 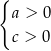
Każdy kąt wewnętrzny sześciokąta 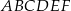 ma miarę
ma miarę 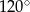 . Bok
. Bok 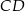 tego sześciokąta jest zwarty w prostej o równaniu
tego sześciokąta jest zwarty w prostej o równaniu 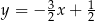 , a punkt
, a punkt 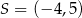 jest środkiem boku
jest środkiem boku 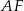 . Bok
. Bok 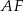 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu
A) 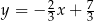 B)
B) 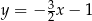 C)
C) 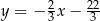 D)
D) 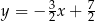
Dziedziną funkcji 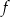 jest przedział
jest przedział 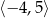 . Poniżej zamieszczono wykres tej funkcji.
. Poniżej zamieszczono wykres tej funkcji.
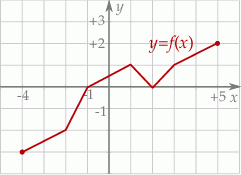
W którym ze zbiorów funkcja 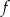 jest rosnąca?
jest rosnąca?
A) 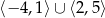 B)
B) 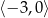 C)
C) 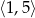 D)
D) 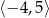
Ciąg 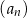 jest określony wzorem
jest określony wzorem 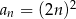 dla
dla 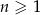 . Różnica
. Różnica 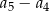 jest równa
jest równa
A) 4 B) 20 C) 36 D) 18
Kąt  jest kątem ostrym takim, że
jest kątem ostrym takim, że 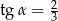 . Zatem
. Zatem
A) 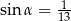 i
i 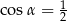 B)
B) 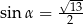 i
i 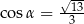
C) 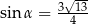 i
i 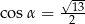 D)
D) 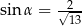 i
i 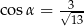
Pole figury ograniczonej prostymi 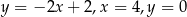 i
i 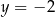 jest równe
jest równe
A) 5 B) 10 C) 7 D) 4
W rozwinięciu dziesiętnym ułamka 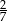 na czterdziestym miejscu po przecinku stoi cyfra
na czterdziestym miejscu po przecinku stoi cyfra
A) 7 B) 1 C) 2 D) 4
Punkt 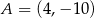 oraz jego rzuty prostokątne na osie układu współrzędnych są wierzchołkami trójkąta prostokątnego. Prosta zawierająca przeciwprostokątną tego trójkąta jest określona równaniem
oraz jego rzuty prostokątne na osie układu współrzędnych są wierzchołkami trójkąta prostokątnego. Prosta zawierająca przeciwprostokątną tego trójkąta jest określona równaniem
A) 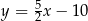 B)
B) 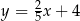 C)
C) 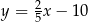 D)
D) 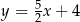
W ciągu arytmetycznym 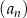 , określonym dla każdej liczby naturalnej
, określonym dla każdej liczby naturalnej 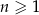 , są dane dwa wyrazy:
, są dane dwa wyrazy: 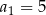 i
i 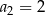 . Stąd wynika, że
. Stąd wynika, że  –ty wyraz tego ciągu jest określony wzorem
–ty wyraz tego ciągu jest określony wzorem
A) 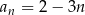 B)
B) 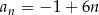 C)
C) 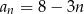 D)
D) 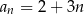
Okrąg o środku 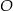 jest styczny do prostej
jest styczny do prostej 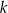 w punkcie
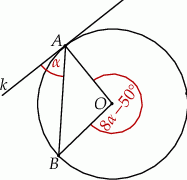
w punkcie 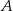 . Miara kąta
. Miara kąta  zaznaczonego na rysunku wynosi:
zaznaczonego na rysunku wynosi:
A) 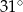 B)
B) 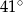 C)
C) 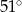 D)
D) 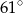
Punkt 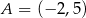 jest końcem odcinka
jest końcem odcinka 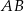 , a punkt
, a punkt 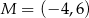 jest takim punktem tego odcinka, że
jest takim punktem tego odcinka, że 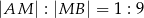 . Długość odcinka
. Długość odcinka 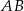 jest równa
jest równa
A) 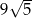 B)
B) 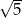 C)
C) 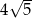 D)
D) 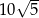
Pole prostokąta 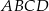 jest równe 90. Na bokach
jest równe 90. Na bokach 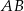 i
i 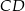 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 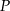 i
i 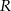 , takie, że
, takie, że 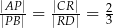 (zobacz rysunek)
(zobacz rysunek)
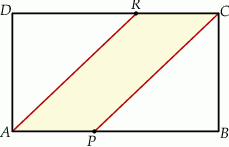
Pole czworokąta 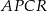 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Dane są punkty 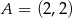 ,
, 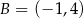 ,
, 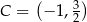 i
i 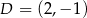 . Pole czworokąta
. Pole czworokąta 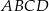 jest równe
jest równe
A) 10,5 B) 16,5 C) 9 D) 8,25
Przekątna graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości tego graniastosłupa. Z tego wynika, że miara kąta, jaki tworzy ta przekątna z podstawą, jest równa
A) 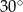 B)
B) 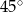 C)
C) 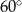 D)
D) 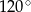
W każdym z pięciu pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 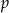 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z pięciu wylosowanych kul będą niebieskie. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z pięciu wylosowanych kul będą niebieskie. Wtedy
A) 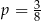 B)
B) 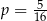 C)
C) 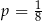 D)
D) 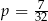
Ile różnych kodów czteroliterowych można utworzyć, przestawiając litery wyrazu MATA ?
A) 24 B) 12 C) 10 D) 8
Na diagramie przedstawione są wyniki pomiaru wzrostu uczniów pewnej klasy.
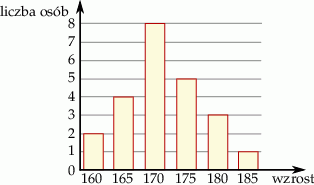
Ile osób w tej klasie ma wzrost poniżej średniego?
A) 14 B) 2 C) 6 D) 19
Zbiór punktów wspólnych kuli i płaszczyzny może być
A) zbiorem dwuelementowym B) okręgiem C) zbiorem jednoelementowym D) sferą
Zadania otwarte
Rozwiąż nierówność 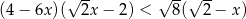 .
.
Rzucamy dwa razy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 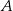 polegającego na tym, że co najwyżej jeden raz wypadnie ścianka z pięcioma oczkami.
polegającego na tym, że co najwyżej jeden raz wypadnie ścianka z pięcioma oczkami.
Rozwiąż równanie 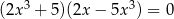 .
.
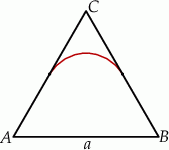
Trójkąt 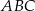 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Wykaż, że łuk okręgu wpisanego w ten trójkąt zawarty między dwoma kolejnymi punktami styczności tego okręgu z bokami trójkąta ma długość większą niż
. Wykaż, że łuk okręgu wpisanego w ten trójkąt zawarty między dwoma kolejnymi punktami styczności tego okręgu z bokami trójkąta ma długość większą niż 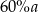 .
.
Wykaż, że jeżeli ciąg 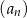 jest ciągiem geometrycznym, to
jest ciągiem geometrycznym, to
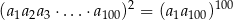
Środki ścian sześcianu są wierzchołkami innej bryły – ośmiościanu foremnego (zobacz rysunek).
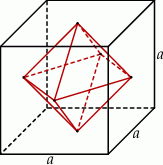
Oblicz objętość tego ośmiościanu jeżeli krawędź sześcianu ma długość  .
.
Prosta o równaniu 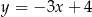 jest symetralną odcinka
jest symetralną odcinka 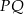 , gdzie
, gdzie 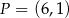 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 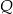 .
.

