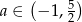Zadanie nr 9129855
Wyznacz wszystkie wartości parametru  , dla których wykresy funkcji
, dla których wykresy funkcji 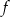 i
i 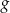 , określonych wzorami
, określonych wzorami 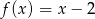 oraz
oraz 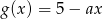 , przecinają się w punkcie o obu współrzędnych dodatnich.
, przecinają się w punkcie o obu współrzędnych dodatnich.
Rozwiązanie
Próbujemy wyznaczyć punkt wspólny wykresów danych funkcji.
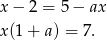
Zauważmy teraz, że jeżeli 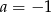 , to powyższe równanie jest sprzeczne (czyli wykresy funkcji
, to powyższe równanie jest sprzeczne (czyli wykresy funkcji 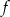 i
i 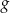 nie mają punktów wspólnych), a jeżeli
nie mają punktów wspólnych), a jeżeli 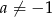 , to
, to
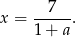
Druga współrzędna punktu przecięcia jest wtedy równa
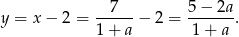
Zauważmy jeszcze, że jeżeli 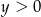 , to automatycznie
, to automatycznie 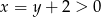 . wystarczy więc rozwiązać nierówność
. wystarczy więc rozwiązać nierówność
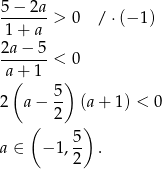
Odpowiedź: