/Szkoła średnia

Zadanie nr 9130944

Dodaj do ulubionych
Dodaj do rozwiązanych

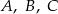Punkty A , B, C leżą na okręgu o środku 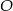O i dzielą ten okrąg na trzy łuki, których stosunek długości jest równy 3:4:5. Oblicz miary kątów trójkąta ABC .

PIC

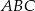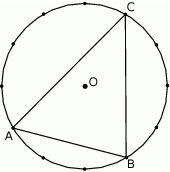
Rozwiązanie

Jeżeli podzielimy okrąg tak jak na obrazku na 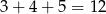3 + 4+ 5 = 12 równych części,

PIC

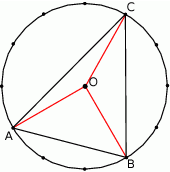
to kąt środkowy oparty na jednym małym łuku ma miarę

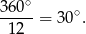
∘ 360-- = 30∘. 12

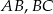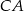Zatem kąty środkowe oparte na łukach AB ,BC i CA mają odpowiednio miary

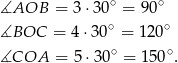
∘ ∘ ∡AOB = 3⋅ 30 = 90 ∡BOC = 4⋅30 ∘ = 120∘ ∘ ∘ ∡COA = 5⋅ 30 = 150 .

Ponieważ kąt wpisany jest równy połowie kąta środkowego opisanego na tym samym łuku, to kąty trójkąta 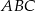ABC wynoszą

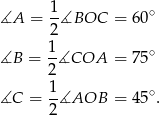
∡A = 1∡BOC = 60∘ 2 1- ∘ ∡B = 2∡COA = 75 1 ∡C = -∡AOB = 45∘. 2

 
Odpowiedź: 60∘,7 5∘,45∘

Wersja PDF