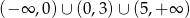/Szkoła średnia

Zadanie nr 9215430

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 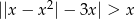2 ||x− x |− 3x | > x .

Rozwiązanie

Zauważmy, że jeżeli 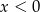x < 0 to nierówność jest na pewno spełniona bo prawa strona jest ujemna. Dla 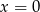x = 0 mamy sprzeczną nierówność 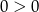0 > 0 , więc załóżmy dalej, że x > 0 .

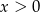Przy tym założeniu mamy 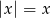|x| = x i możemy wyłączyć x przed znak wartości bezwzględnej z lewej strony.

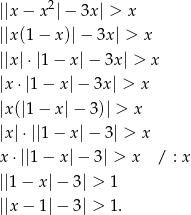
||x − x 2|− 3x| > x ||x (1− x )|− 3x | > x ||x |⋅|1− x|− 3x | > x |x⋅|1 − x| − 3x| > x |x(|1− x |− 3)| > x |x|⋅||1− x|− 3| > x x ⋅||1 − x| − 3| > x / : x ||1 − x| − 3| > 1 ||x − 1| − 3| > 1.

W ostatnim przejściu skorzystaliśmy z równości 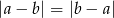|a− b| = |b − a| . Przekształcamy dalej

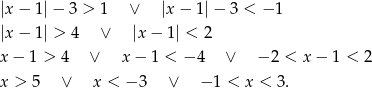
|x − 1| − 3 > 1 ∨ |x − 1| − 3 < − 1 |x − 1| > 4 ∨ |x − 1| < 2 x− 1 > 4 ∨ x − 1 < −4 ∨ − 2 < x − 1 < 2 x > 5 ∨ x < − 3 ∨ − 1 < x < 3 .

Uwzględniając założenie 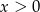x > 0 otrzymujemy stąd x ∈ (0,3) ∪ (5,+ ∞ ) .

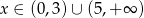Uwzględniając przypadek 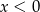x < 0 , zbiorem rozwiązań nierówności jest

(−∞ ,0 )∪ (0,3) ∪ (5,+ ∞ ).

 
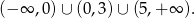
Odpowiedź: (− ∞ ,0) ∪ (0,3)∪ (5 ,+ ∞ )

Wersja PDF