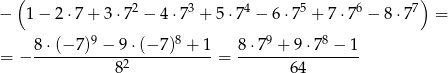Zadanie nr 9220610
Korzystając ze wzoru
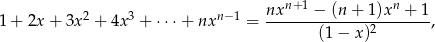
który jest prawdziwy dla dowolnej liczby naturalnej  i dowolnej liczby
i dowolnej liczby 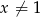 , wykaż, że
, wykaż, że
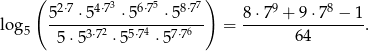
Rozwiązanie
Przekształćmy podane wyrażenie
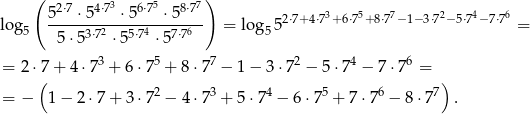
No i w końcu możemy zastosować podany wzór (z 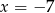 i
i 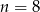 ).
).
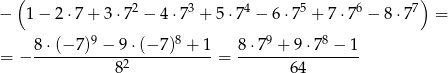
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Korzystając ze wzoru
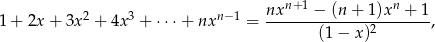
który jest prawdziwy dla dowolnej liczby naturalnej  i dowolnej liczby
i dowolnej liczby 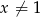 , wykaż, że
, wykaż, że
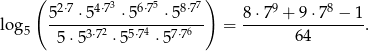
Przekształćmy podane wyrażenie
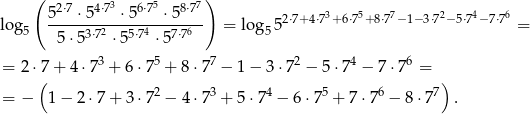
No i w końcu możemy zastosować podany wzór (z 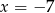 i
i 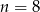 ).
).