/Szkoła średnia

Zadanie nr 9241977

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczba miejsc zerowych funkcji 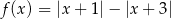f (x) = |x+ 1|− |x + 3| , gdzie 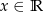x ∈ R jest równa
A) 3 B) 2 C) 1 D) 0

Rozwiązanie

Sposób I

Przekształcamy równanie

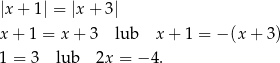
|x + 1| = |x + 3| x+ 1 = x + 3 lub x + 1 = − (x + 3) 1 = 3 lub 2x = − 4.

Funkcja 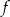f ma więc jedno miejsce zerowe x = − 2 .

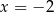Sposób II

Opuszczamy wartości bezwzględne w zależności od wartości x .

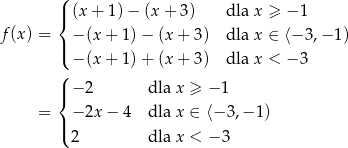
( |{ (x+ 1)− (x+ 3) dla x ≥ − 1 f(x) = | − (x + 1)− (x + 3) dla x ∈ ⟨− 3,− 1) ( − (x + 1)+ (x + 3) dla x < − 3 ( |{ − 2 dla x ≥ − 1 = − 2x− 4 dla x ∈ ⟨− 3,− 1) |( 2 dla x < − 3

Widać teraz, że funkcja 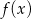f (x) ma jedno miejsce zerowe x = − 2 .

PIC

 
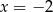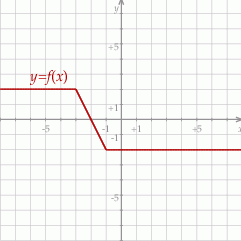
Odpowiedź: C

Wersja PDF