Zadanie nr 9244632
Ze zbioru 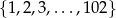 losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
Rozwiązanie
Ustalmy, że zdarzenia sprzyjające to nieuporządkowane pary wylosowanych liczb. Zatem
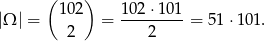
W podanym przedziale mamy następujące liczby podzielne przez 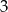
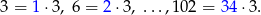
Jest ich zatem 34. Podobnie liczymy liczby, których reszty z dzielenia przez 3 wynoszą 1 i 2 odpowiednio.
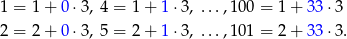
Jednych i drugich jest więc 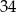 .
.
Jeżeli suma wylosowanych liczb ma dzielić się przez 3, to albo obie są podzielne przez 3 – mamy na to
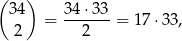
lub jedna daje resztę 1, a druga 2 – mamy na to
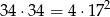
możliwości. Stąd
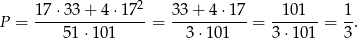
Odpowiedź: