Zadanie nr 9244706
Rozwiąż nierówność 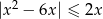 .
.
Rozwiązanie
Sposób I
Jeżeli 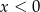 , to podana nierówność nie ma rozwiązań. Możemy zatem założyć, że
, to podana nierówność nie ma rozwiązań. Możemy zatem założyć, że 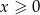 . Podana nierówność jest równoważna dwóm nierównościom
. Podana nierówność jest równoważna dwóm nierównościom
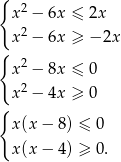
Rozwiązaniem pierwszej z tych nierówności jest przedział 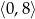 , a drugiej
, a drugiej 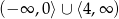 . Część wspólna tych dwóch zbiorów to
. Część wspólna tych dwóch zbiorów to
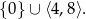
Sposób II
Nierówność możemy też rozwiązać graficznie. Wykres funkcji 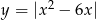 otrzymujemy z paraboli
otrzymujemy z paraboli 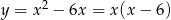 (o miejscach zerowych 0,6 i wierzchołku w punkcie
(o miejscach zerowych 0,6 i wierzchołku w punkcie 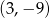 ) przez odbicie części poniżej osi
) przez odbicie części poniżej osi 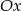 do góry.
do góry.
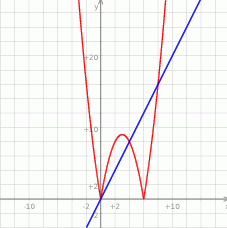
Jeżeli na tym samym wykresie narysujemy prostą 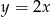 to widać, że wykresy te przecinają się w trzech punktach. Przy odręcznym rysunku możemy zgadnąć i sprawdzić punkt
to widać, że wykresy te przecinają się w trzech punktach. Przy odręcznym rysunku możemy zgadnąć i sprawdzić punkt 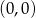 . Pozostałe dwa łatwo wyliczyć. Zakładając, że
. Pozostałe dwa łatwo wyliczyć. Zakładając, że 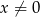 mamy
mamy
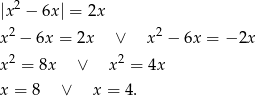
Teraz łatwo z wykresu odczytać zbiór, na którym parabola jest poniżej prostej:
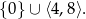
Odpowiedź: