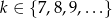Zadanie nr 9251303
Ciąg 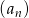 , gdzie
, gdzie 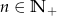 , określony jest następująco:
, określony jest następująco:
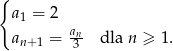
Wyznacz wszystkie wartości 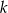 , dla których suma
, dla których suma 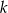 początkowych wyrazów ciągu
początkowych wyrazów ciągu 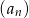 jest większa od
jest większa od 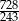 .
.
Rozwiązanie
Z określenia ciągu 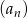 jest jasne, że jest to ciąg geometryczny o ilorazie
jest jasne, że jest to ciąg geometryczny o ilorazie 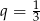 . Ze wzoru na sumę początkowych wyrazów ciągu geometrycznego mamy więc do rozwiązania nierówność.
. Ze wzoru na sumę początkowych wyrazów ciągu geometrycznego mamy więc do rozwiązania nierówność.
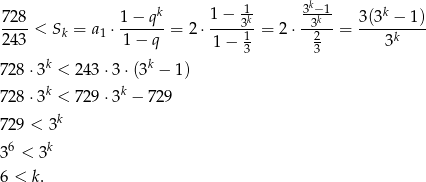
Odpowiedź: