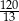Zadanie nr 9255027
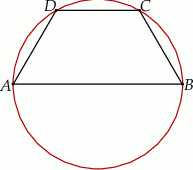
W okrąg wpisano trapez równoramienny 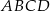 w ten sposób, że podstawa
w ten sposób, że podstawa 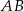 jest średnicą tego okręgu. Ramię trapezu ma długość 10, a jego przekątna jest o 11 dłuższa od promienia okręgu. Oblicz wysokość tego trapezu.
jest średnicą tego okręgu. Ramię trapezu ma długość 10, a jego przekątna jest o 11 dłuższa od promienia okręgu. Oblicz wysokość tego trapezu.
Rozwiązanie
Dorysujmy przekątną i wysokość trapezu.
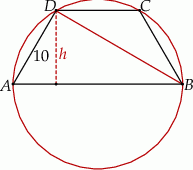
Zauważmy, że kąt 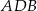 jest opisany na średnicy, więc trójkąt
jest opisany na średnicy, więc trójkąt 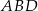 jest prostokątny. Jeżeli oznaczymy przez
jest prostokątny. Jeżeli oznaczymy przez  promień okręgu, to
promień okręgu, to 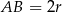 i
i 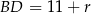 . Piszemy teraz twierdzenie Pitagorasa w tym trójkącie.
. Piszemy teraz twierdzenie Pitagorasa w tym trójkącie.
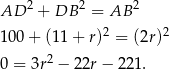
Rozwiązujemy otrzymane równanie kwadratowe.
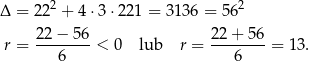
Zatem 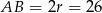 i
i 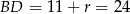 .
.
Pozostało obliczyć wysokość trapezu – liczymy pole trójkąta  na dwa sposoby.
na dwa sposoby.
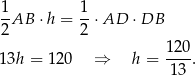
Odpowiedź: