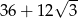/Szkoła średnia

Zadanie nr 9274850

Dodaj do ulubionych
Dodaj do rozwiązanych

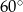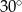W trapezie kąty przy dłuższej podstawie to ∘ 60 i ∘ 30 , a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.

Rozwiązanie

Zaczynamy od rysunku

PIC

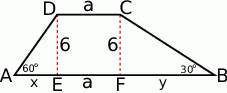
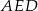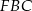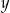Widać, że z trójkątów prostokątnych AED i F BC można łatwo wyliczyć długości odcinków x i y oraz długości ramion.

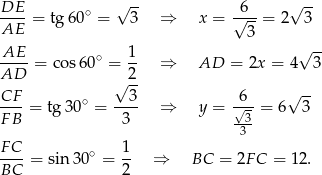
-- -- DE--= tg6 0∘ = √ 3 ⇒ x = √6--= 2 √ 3 AE 3 AE 1 √ -- ---- = co s60∘ = -- ⇒ AD = 2x = 4 3 AD √ 2- CF-- ∘ --3- -6- √ -- F B = tg 30 = 3 ⇒ y = √-3 = 6 3 3 F C ∘ 1 ----= sin 30 = -- ⇒ BC = 2FC = 12. BC 2

Pozostało skorzystać teraz z równości sum długości ramion i podstaw.

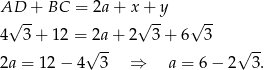
AD + BC = 2a+ x+ y √ -- √ -- √ -- 4 3 + 12 = 2a + 2 3+ 6 3 2a = 12 − 4 √ 3- ⇒ a = 6 − 2√ 3.

Zatem druga podstawa ma długość

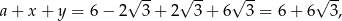
√ -- √ -- √ -- √ -- a+ x + y = 6− 2 3 + 2 3 + 6 3 = 6+ 6 3,

a pole jest równe

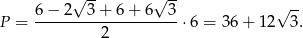
√ -- √ -- √ -- P = 6-−-2--3-+-6-+-6--3-⋅6 = 36+ 12 3. 2

 
Odpowiedź: Podstawy: 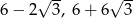√ -- √ -- 6 − 2 3 , 6 + 6 3 , pole √ -- 36 + 12 3

Wersja PDF