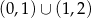Zadanie nr 9279322
Dla jakich wartości parametru 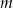 , równanie
, równanie 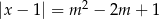 ma dwa pierwiastki dodatnie?
ma dwa pierwiastki dodatnie?
Rozwiązanie
Dane równanie ma postać
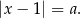
Jakie musi być  , żeby to równanie miało dwa rozwiązania dodatnie? Jeden ze sposobów na znalezienie odpowiedzi, to narysowanie wykresu
, żeby to równanie miało dwa rozwiązania dodatnie? Jeden ze sposobów na znalezienie odpowiedzi, to narysowanie wykresu 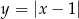 , czyli funkcji
, czyli funkcji 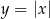 przesuniętej o jedną jednostkę w prawo.
przesuniętej o jedną jednostkę w prawo.
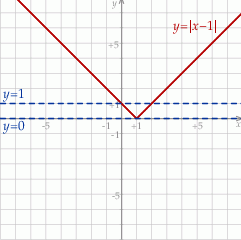
Z tego wykresu jest jasne, że równanie 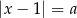 ma dwa rozwiązania dodatnie tylko dla
ma dwa rozwiązania dodatnie tylko dla 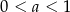 .
.
Jeżeli ktoś wolałby to obliczyć zamiast odczytywać z wykresu, to równanie to ma dwa rozwiązania tylko dla 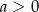 – te rozwiązania to
– te rozwiązania to
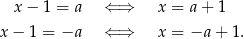
Są one dodatnie tylko dla
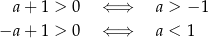
co daje tę samą odpowiedź co poprzednio (bo 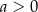 ).
).
Pozostało rozwiązać nierówność (a w zasadzie dwie) kwadratową
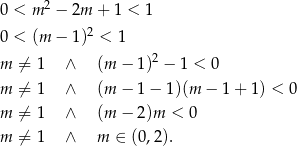
Odpowiedź: