/Szkoła średnia

Zadanie nr 9292895

Dodaj do ulubionych
Dodaj do rozwiązanych

Narysuj linię o równaniu 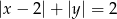|x − 2|+ |y| = 2 i oblicz jej długość.

Rozwiązanie

Sposób I

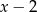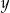W zależności od znaków wyrażeń x − 2 i y , podane równanie przyjmuje postać

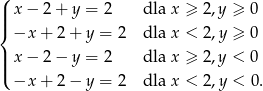
( x − 2 + y = 2 dla x ≥ 2,y ≥ 0 |||{ −x + 2 + y = 2 dla x < 2,y ≥ 0 | x − 2 − y = 2 dla x ≥ 2,y < 0 ||( −x + 2 − y = 2 dla x < 2,y < 0 .

W każdym z przypadków łatwo zamienić warunek na 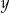y na odpowidający warunek na x , np. w pierwszym przypadku

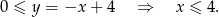
0 ≤ y = −x + 4 ⇒ x ≤ 4.

Postępując w podobny sposób w pozostałych przypadkach, równanie przyjmuje postać.

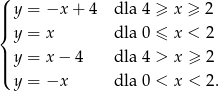
( ||| y = −x + 4 dla 4 ≥ x ≥ 2 { y = x dla 0 ≤ x < 2 | y = x − 4 dla 4 > x ≥ 2 ||( y = −x dla 0 < x < 2 .

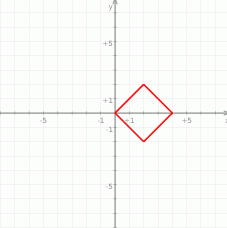
Teraz bez trudu rysujemy tę krzywą – wyjdzie kwadrat o wierzchołkach

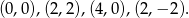
(0,0),(2,2),(4,0),(2,− 2).

Bok tego kwadratu ma długość 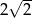2√ 2- , zatem ma on obwód 8√ 2- .

PIC

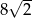Sposób II

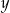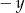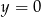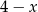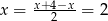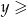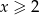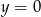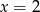Widać, że podane równanie nie zmienia się przy zamianie y na − y , to oznacza, że odpowiadający my wykres jest symetryczny względem prostej y = 0 . Podobnie, równanie nie zmienia się przy zamianie x na 4− x , co oznacza, że wykres jest symetryczny względem prostej x+ 4−x x = ---2-- = 2 . Zatem wystarczy go narysować dla y ≥ i x ≥ 2 , a potem poodbijać względem prostych y = 0 i x = 2 . Długość liczymy jak poprzednio.  
Odpowiedź: Obwód: √ -- 8 2

Wersja PDF