Zadanie nr 9296688
Suma długości przyprostokątnych trójkąta prostokątnego jest równa 7. Jaka jest najmniejsza możliwa długość przeciwprostokątnej tego trójkąta?
Rozwiązanie
Szkicujemy trójkąt prostokątny.
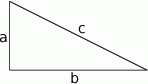
Z założenia 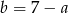 , więc
, więc
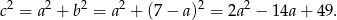
Wykresem otrzymanego wyrażenia jest parabola o ramionach skierowanych w górę i wierzchołku w punkcie
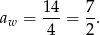
W takim razie najmniejszą możliwą wartość  otrzymamy dla
otrzymamy dla 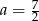 . Wtedy
. Wtedy 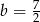 i
i
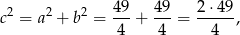
czyli 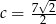 .
.
Odpowiedź: