/Szkoła średnia

Zadanie nr 9300189

Dodaj do ulubionych
Dodaj do rozwiązanych

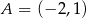Punkt A = (− 2,1) jest wierzchołkiem rombu o polu równym 20. Punkt 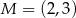M = (2,3) jest środkiem symetrii tego rombu. Wyznacz równanie okręgu wpisanego w ten romb.

Rozwiązanie

Zaczynamy od schematycznego rysunku.

PIC

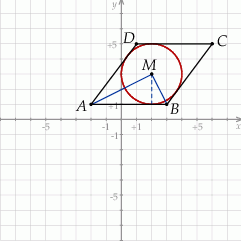
Środkiem szukanego okręgu jest punkt 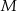M , pozostało zatem wyznaczyć jego promień. Z podanych informacji możemy łatwo wyliczyć długość przekątnej 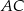AC rombu:

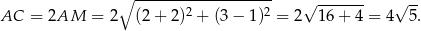
∘ ------------------- 2 2 √ ------- √ -- AC = 2AM = 2 (2 + 2 ) + (3 − 1) = 2 16+ 4 = 4 5.

Z podanego pola, i ze wzoru na pole rombu z przekątnymi, możemy wyliczyć długość drugiej przekątnej.

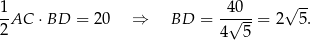
-- 1AC ⋅BD = 20 ⇒ BD = -4√0--= 2√ 5. 2 4 5

Ponieważ przekątne rombu są prostopadłe, trójkąt 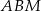ABM jest prostokątny i znamy długości jego przyprostokątnych. Policzmy długość jego przeciwprostokątnej.

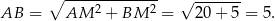
∘ ----2-------2 √ ------- AB = AM + BM = 20 + 5 = 5.

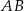Porównując teraz dwa wzory na pole, możemy wyliczyć długość r jego wysokości opuszczonej na bok AB (czyli szukany promień okręgu wpisanego w romb).

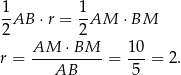
1 1 -AB ⋅r = --AM ⋅BM 2 2 r = AM--⋅-BM--= 10-= 2. AB 5

Zatem szukane równanie okręgu jest następujące

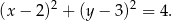
(x − 2)2 + (y − 3)2 = 4.

 
Odpowiedź: (x − 2)2 + (y − 3)2 = 4

Wersja PDF