Zadanie nr 9308279
Oblicz prawdopodobieństwo, że w czterech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 5.
Rozwiązanie
Za zdarzenia elementarne przyjmijmy ciągi wyników, czyli
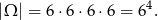
Obliczmy teraz, ile jest zdarzeń sprzyjających.
Zauważmy najpierw, że kwadrat liczby całkowitej zawsze daje resztę 0, 1 lub 4 przy dzieleniu przez 5. Rzeczywiście, jeżeli 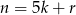 , gdzie
, gdzie 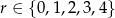 , to
, to
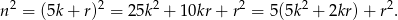
Podstawiając teraz za  kolejno 0, 1, 2, 3, 4 otrzymujemy
kolejno 0, 1, 2, 3, 4 otrzymujemy
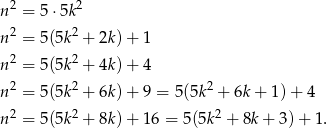
Zastanówmy się teraz w jaki sposób suma kwadratów czterech liczb
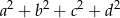
może dawać liczbę podzielną przez 5 – myślimy o resztach jakie dają liczby 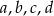 przy dzieleniu przez 5. Zauważmy, że każdej jedynce w tym wyrażeniu musi odpowiadać czwórka i odwrotnie, każdej czwórce musi odpowiadać jedynka. Oprócz tego może być oczywiście dowolna liczba zer. W takim razie jedyne możliwe układy reszt to
przy dzieleniu przez 5. Zauważmy, że każdej jedynce w tym wyrażeniu musi odpowiadać czwórka i odwrotnie, każdej czwórce musi odpowiadać jedynka. Oprócz tego może być oczywiście dowolna liczba zer. W takim razie jedyne możliwe układy reszt to
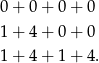
Pierwszemu układowi reszt odpowiada jedno zdarzenie sprzyjające: 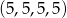 . W drugim układzie reszt musimy wybrać miejsce dla dwóch piątek – możemy to zrobić na
. W drugim układzie reszt musimy wybrać miejsce dla dwóch piątek – możemy to zrobić na
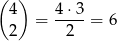
sposobów. Potem na trzy sposoby wybieramy liczbę, której kwadrat da resztę 1 (może to być: 1, 4, 6), potem na dwa sposoby wybieramy liczbę, która da resztę 4 (może to być 2 lub 3) i umieszczamy te dwie wybrane liczby na 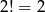 sposoby na pozostałych dwóch miejscach. W sumie w tym przypadku są więc
sposoby na pozostałych dwóch miejscach. W sumie w tym przypadku są więc
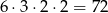
zdarzenia sprzyjające.
W ostatnim układzie reszt musimy wybrać dwa miejsca dla reszt równych 1 – możemy to zrobić na
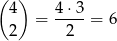
sposobów. Potem na tych miejscach umieszczamy na
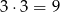
sposobów liczby spośród: 1, 4, 6 (czyli takie, których kwadrat daje resztę 1). Na koniec na pozostałych dwóch miejscach na
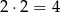
sposoby umieszczamy liczby spośród 2 i 3 (czyli takie, których kwadrat daje resztę 4). W sumie w tym przypadku jest więc
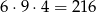
zdarzeń sprzyjających. Prawdopodobieństwo jest więc równe
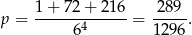
Odpowiedź: