/Szkoła średnia

Zadanie nr 9310473

Dodaj do ulubionych
Dodaj do rozwiązanych

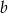Wyznacz współczynniki a i b funkcji kwadratowej 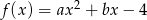2 f(x) = ax + bx − 4 , jeśli współrzędne wierzchołka wynoszą 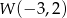W (− 3,2) . Przedstaw trójmian w postaci iloczynowej.

Rozwiązanie

Najprościej jest skorzystać z postaci kanonicznej 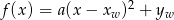2 f(x) = a(x− xw) + yw . Podane współrzędne wierzchołka dają nam wzór

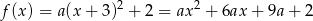
f(x) = a(x + 3 )2 + 2 = ax2 + 6ax + 9a + 2

Podany wyraz wolny 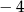− 4 daje nam równanie

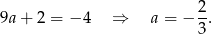
9a + 2 = − 4 ⇒ a = − 2-. 3

Zatem

b = 6a = − 4

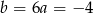
i wielomian ma wzór 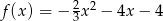2 2 f(x) = − 3x − 4x − 4 . Postać iloczynową łatwo otrzymać z postaci kanonicznej lub ze wzorów na pierwiastki. My zrobimy to pierwszą z metod.

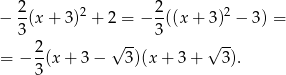
2- 2 2- 2 − 3 (x + 3) + 2 = − 3((x + 3) − 3) = 2 √ -- √ -- = − --(x+ 3− 3)(x + 3 + 3). 3

 
Odpowiedź: 2 √ -- √ -- − 3(x + 3 − 3)(x + 3 + 3 )

Wersja PDF