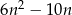/Szkoła średnia

Zadanie nr 9311444

Dodaj do ulubionych
Dodaj do rozwiązanych

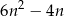W ciągu arytmetycznym suma n początkowych wyrazów o numerach parzystych jest równa 6n2 − 4n . Oblicz sumę n początkowych wyrazów o numerach nieparzystych.

Rozwiązanie

Z podanego wzoru na sumę n początkowych wyrazów o numerach parzystych mamy

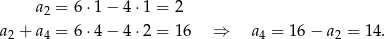
a 2 = 6⋅1 − 4 ⋅1 = 2 a2 + a 4 = 6⋅4 − 4 ⋅2 = 1 6 ⇒ a4 = 16 − a2 = 1 4.

To oznacza, że różnica danego ciągu jest równa

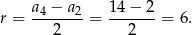
a4-−-a2 14−--2- r = 2 = 2 = 6 .

Sumę n początkowych wyrazów o numerach nieparzystych obliczymy na trzy sposoby.

Sposób I

Zauważmy, że

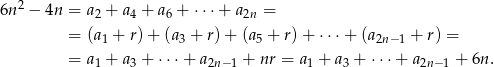
2 6n − 4n = a2 + a4 + a6 + ⋅⋅⋅+ a2n = = (a + r)+ (a + r) + (a + r)+ ⋅⋅⋅+ (a + r) = 1 3 5 2n− 1 = a1 + a3 + ⋅⋅⋅+ a2n− 1 + nr = a1 + a3 + ⋅⋅⋅+ a2n− 1 + 6n.

Stąd

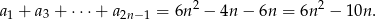
a1 + a3 + ⋅⋅⋅+ a2n−1 = 6n 2 − 4n − 6n = 6n 2 − 10n.

Sposób II

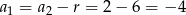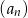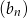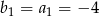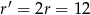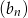Zauważmy najpierw, że a1 = a2 − r = 2 − 6 = − 4 , więc kolejne wyrazy ciągu (an) o numerach nieparzystych tworzą ciąg arytmetyczny (bn) , w którym b1 = a 1 = − 4 i r′ = 2r = 12 . Suma n początkowych wyrazów ciągu (bn) jest równa

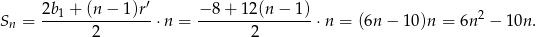
2b1-+-(n-−-1)r′ −-8-+-12-(n−--1) 2 Sn = 2 ⋅n = 2 ⋅n = (6n − 1 0)n = 6n − 1 0n.

Sposób III

Jak poprzednio zauważamy, że 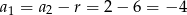a = a − r = 2 − 6 = − 4 1 2 , więc suma 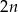2n początkowych wyrazów ciągu 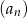(an) jest równa

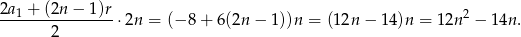
2a 1 + (2n − 1)r ----------------⋅ 2n = (− 8 + 6(2n − 1 ))n = (12n − 1 4)n = 12n 2 − 14n. 2

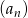To oznacza, że suma n początkowych wyrazów ciągu (an ) o numerach nieparzystych jest równa

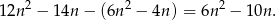
2 2 2 12n − 14n − (6n − 4n) = 6n − 10n.

 
Odpowiedź: 6n 2 − 1 0n

Wersja PDF