/Szkoła średnia

Zadanie nr 9312424

Dodaj do ulubionych
Dodaj do rozwiązanych

Z urny, w której jest 6 kul czarnych i 4 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule jednakowych kolorów.

Rozwiązanie

Najpierw obliczmy na ile sposobów możemy wyciągnąć 2 kule

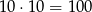
10⋅1 0 = 100

(kule zwracamy więc za każdym razem losujemy spośród 10 kul).

Sposób I

Zastanówmy się jakie będą zdarzenia sprzyjające. Po pierwsze, możemy wyciągnąć 2 kule czarne. Możemy zrobić to na

6 ⋅6 = 36

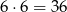
sposobów. Druga możliwa sytuacja to wylosowanie 2 kul żółtych. Możemy zrobić to na

4 ⋅4 = 16

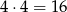
sposobów. Zatem prawdopodobieństwo wynosi

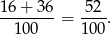
1-6+--36 -52- 1 00 = 1 00.

Sposób II

Obliczymy prawdopodobieństwo zdarzenia przeciwnego tzn. prawdopodobieństwo wylosowania kul różnych kolorów. Możemy to zrobić na

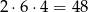
2⋅ 6⋅4 = 48

sposobów (mnożymy przez dwa, bo możemy wylosować kulę czarną a następnie żółtą, albo najpierw żółtą, a później czarną). Zatem prawdopodobieństwo wylosowania kul tego samego koloru wynosi

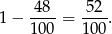
48 52 1 − ---- = ----. 1 00 1 00

 
Odpowiedź: -52 100 = 0,5 2

Wersja PDF