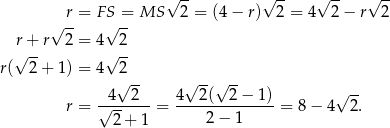Zadanie nr 9313459
Na rysunku przedstawiono dwa kwadraty: 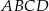 i
i 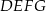 , przy czym punkty
, przy czym punkty 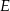 i
i 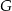 należą do odcinków
należą do odcinków 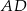 i
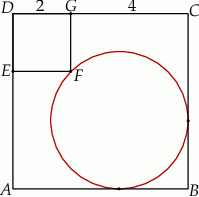
i 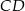 odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu
odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu 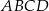 i przechodzi przez punkt
i przechodzi przez punkt 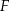 . Wykaż, że jeżeli
. Wykaż, że jeżeli 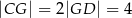 , to promień okręgu jest równy
, to promień okręgu jest równy 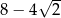 .
.
Rozwiązanie
Niech 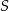 będzie środkiem danego okręgu, a
będzie środkiem danego okręgu, a 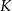 punktem jego styczności z odcinkiem
punktem jego styczności z odcinkiem 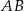 .
.
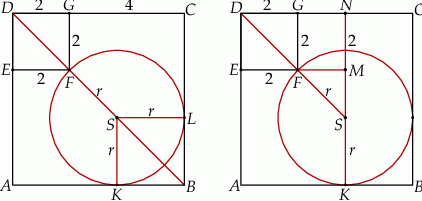
Sposób I
Jeżeli 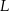 jest punktem styczności okręgu z bokiem
jest punktem styczności okręgu z bokiem 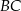 , to
, to 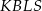 jest kwadratem o boku
jest kwadratem o boku  , więc
, więc
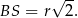
Stąd
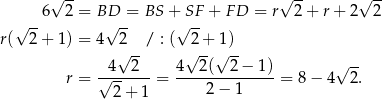
Sposób II
Tym razem, niech 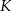 i
i 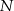 będą rzutami punktu
będą rzutami punktu 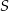 na odcinki
na odcinki 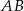 i
i 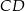 odpowiednio, oraz
odpowiednio, oraz 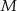 niech będzie rzutem punktu
niech będzie rzutem punktu 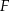 na prostą
na prostą 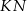 .
.
Trójkąt prostokątny 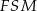 jest równoramienny (jest to połówka kwadratu) oraz
jest równoramienny (jest to połówka kwadratu) oraz
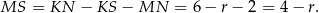
Mamy zatem