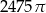/Szkoła średnia

Zadanie nr 9320457

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz sumę stu najmniejszych dodatnich rozwiązań równania 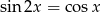sin 2x = cos x .

Rozwiązanie

Rozwiążmy najpierw podane równanie.

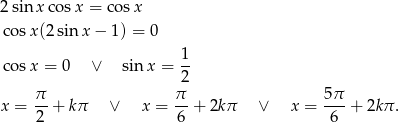
2sin xcos x = co sx cos x(2sin x − 1) = 0 1 cos x = 0 ∨ sin x = -- 2 x = π- + kπ ∨ x = π-+ 2kπ ∨ x = 5π-+ 2kπ . 2 6 6

Rozwiązania te układają nam się w 3 ciągi arytmetyczne

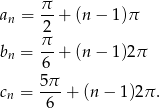
π an = --+ (n − 1 )π 2 bn = π-+ (n − 1 )2π 6 5-π cn = 6 + (n − 1 )2π.

Mamy przy tym

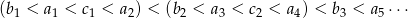
(b1 < a1 < c1 < a 2) < (b2 < a3 < c2 < a4) < b 3 < a5⋅⋅⋅

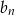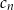Aby otrzymać 100 wyrazów, musimy mieć 25 takich nawiasów, czyli 25 wyrazów ciągów b n i c n oraz 50 wyrazów ciągu 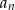a n . Musimy więc policzyć

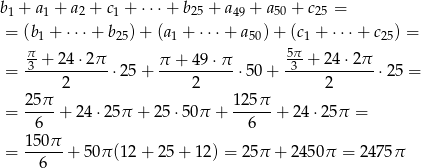
b + a + a + c + ⋅ ⋅⋅+ b + a + a + c = 1 1 2 1 25 49 50 25 = (b1 + ⋅⋅⋅+ b25)+ (a 1 + ⋅⋅ ⋅+ a50)+ (c1 + ⋅ ⋅⋅+ c25) = π-+ 24 ⋅2π 5π-+ 2 4⋅2π = 3----------⋅ 25+ π-+-4-9⋅π--⋅50+ -3-----------⋅25 = 2 2 2 25π- 125π-- = 6 + 24⋅2 5π + 25 ⋅50π + 6 + 24 ⋅25π = 150π = -----+ 50π (12+ 25+ 12) = 25π + 2450 π = 2 475π 6

 
Odpowiedź: 247 5π

Wersja PDF