Zadanie nr 9321191
Wykaż, że dla dowolnego kąta ostrego  , wartość wyrażenia
, wartość wyrażenia 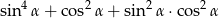 jest stała.
jest stała.
Rozwiązanie
Przekształcamy dane wyrażenie korzystając z jedynki trygonometrycznej.
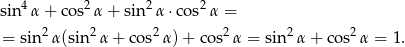
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla dowolnego kąta ostrego  , wartość wyrażenia
, wartość wyrażenia 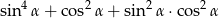 jest stała.
jest stała.
Przekształcamy dane wyrażenie korzystając z jedynki trygonometrycznej.