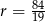/Szkoła średnia

Zadanie nr 9336781

Dodaj do ulubionych
Dodaj do rozwiązanych

Trójkąt prostokątny o przyprostokątnych długości 12 i 7 obraca się wokół przeciwprostokątnej. Oblicz promień kuli wpisanej w otrzymaną bryłę.

Rozwiązanie

Rozpoczynamy od rysunku – od razu rysujemy przekrój osiowy.

PIC

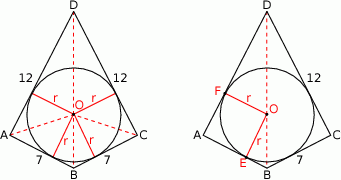
Sposób I

Zauważmy, że pole czworokąta ABCD jest równe sumie pól trójkątów AOB ,BOC ,COD ,DOA . Zatem

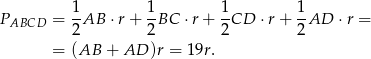
P = 1-AB ⋅r+ 1BC ⋅r+ 1CD ⋅r + 1-AD ⋅r = ABCD 2 2 2 2 = (AB + AD )r = 19r.

Z drugiej strony możemy to pole obliczyć jako sumę pól dwóch trójkątów prostokątnych 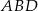ABD i BCD .

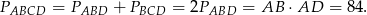
PABCD = PABD + PBCD = 2PABD = AB ⋅AD = 84 .

Zatem

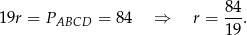
84 19r = PABCD = 84 ⇒ r = --. 19

Sposób II

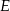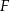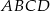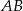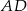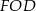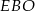Niech E i F będą punktami styczności okręgu wpisanego w czworokąt ABCD z bokami AB i AD . Zauważmy teraz, że każdy z trójkątów F OD i EBO jest prostokątny i każdy z nich ma kąt wspólny z trójkątem 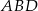ABD . Zatem każdy z nich jest podobny do trójkąta 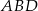ABD . Z tego podobieństwa mamy

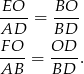
-EO- BO-- AD = BD F O OD ---- = ----. AB BD

Dodajemy te równości stronami.

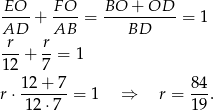
EO FO BO + OD ----+ ----= ----------= 1 ArD r AB BD ---+ --= 1 12 7 r ⋅ 12-+-7-= 1 ⇒ r = 8-4. 12⋅ 7 1 9

 
Odpowiedź: r = 84 19

Wersja PDF