Zadanie nr 9337481
Wyznacz zbiór wartości funkcji 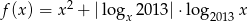 .
.
Rozwiązanie
Ponieważ  występuje w podstawie logarytmu, musi być
występuje w podstawie logarytmu, musi być 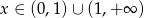 . Na mocy wzoru na zmianę podstawy logarytmu mamy
. Na mocy wzoru na zmianę podstawy logarytmu mamy
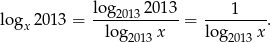
Wzór funkcji 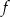 możemy więc zapisać w postaci
możemy więc zapisać w postaci
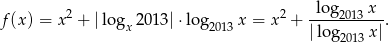
Aby opuścić wartość bezwzględną zauważmy, że 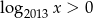 dla
dla 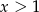 i
i 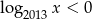 dla
dla 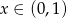 . Mamy zatem
. Mamy zatem
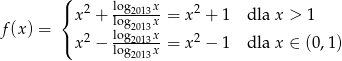
Wygodnie jest teraz naszkicować wykres funkcji 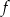 .
.
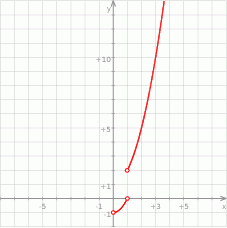
Z wykresu widać, że zbiorem wartości funkcji 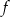 jest zbiór
jest zbiór 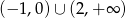 .
.
Odpowiedź: