/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 23 marca 2019 Czas pracy: 180 minut
Zadania zamknięte
Ile liczb pierwszych spełnia nierówność 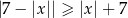 ?
?
A) 0 B) 1 C) 2 D) nieskończenie wiele
W trójkącie równoramiennym 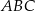 o podstawie
o podstawie 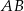 dane są:
dane są: 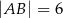 oraz
oraz 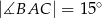 . Pole koła opisanego na tym trójkącie jest równe
. Pole koła opisanego na tym trójkącie jest równe
A) 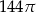 B)
B) 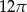 C)
C) 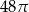 D)
D) 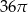
Liczba 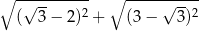 jest równa
jest równa
A) 1 B) 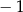 C)
C) 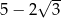 D)
D) 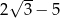
Okresem podstawowym funkcji 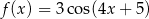 określonej dla
określonej dla 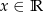 jest liczba
jest liczba
A) 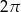 B)
B) 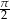 C)
C) 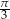 D)
D) 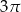
Ciąg 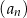 określony jest w następujący sposób
określony jest w następujący sposób 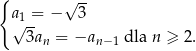 Suma wszystkich wyrazów ciągu
Suma wszystkich wyrazów ciągu 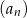 jest równa
jest równa
A) 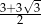 B)
B) 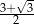 C)
C) 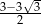 D)
D) 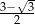
Zadania otwarte
Zdarzenia losowe 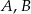 są zawarte w
są zawarte w 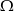 oraz
oraz 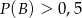 . Wykaż, że
. Wykaż, że
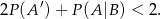
Wykres funkcji 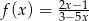 przesunięto o wektor
przesunięto o wektor ![[− 3,2]](https://img.zadania.info/zes/0093461/HzesT31x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 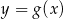 . Oblicz granicę
. Oblicz granicę
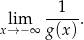
Styczna do paraboli o równaniu 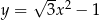 w punkcie
w punkcie 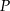 przecina prostą o równaniu
przecina prostą o równaniu 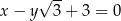 pod kątem
pod kątem 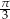 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 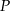 .
.
Udowodnij, że dla dowolnego kąta 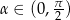 prawdziwa jest nierówność
prawdziwa jest nierówność
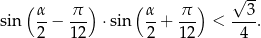
Liczby  i
i 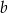 są rozwiązaniami równania
są rozwiązaniami równania 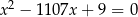 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
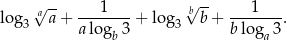
Podstawą prostopadłościanu 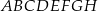 o wysokości 4 jest kwadrat
o wysokości 4 jest kwadrat 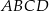 o boku 3. Oblicz sinus kąta, pod którym przecinają się przekątne
o boku 3. Oblicz sinus kąta, pod którym przecinają się przekątne 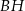 i
i 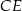 tego prostopadłościanu.
tego prostopadłościanu.
Dany jest nieskończony ciąg sześcianów 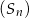 określony dla
określony dla 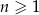 . Krawędź pierwszego z nich jest równa
. Krawędź pierwszego z nich jest równa 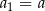 . Krawędź drugiego z tych sześcianów ma długość
. Krawędź drugiego z tych sześcianów ma długość 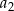 równą różnicy długości przekątnej i przekątnej ściany pierwszego sześcianu. Analogicznie, trzeci sześcian ma krawędź
równą różnicy długości przekątnej i przekątnej ściany pierwszego sześcianu. Analogicznie, trzeci sześcian ma krawędź 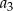 o długości równej różnicy długości przekątnej i przekątnej ściany drugiego sześcianu, itd. Oblicz sumę pól powierzchni wszystkich sześcianów tworzących ciąg
o długości równej różnicy długości przekątnej i przekątnej ściany drugiego sześcianu, itd. Oblicz sumę pól powierzchni wszystkich sześcianów tworzących ciąg 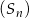 .
.
Do dwóch stycznych zewnętrznie okręgów poprowadzono dwie wspólne styczne: jedną zewnętrzną i jedną wewnętrzną. Proste te przecinają się pod kątem 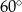 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów.
Wyznacz wszystkie wartości parametrów 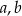 i
i  , dla których wielomian
, dla których wielomian
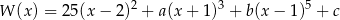
jest podzielny przez wielomian 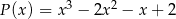 .
.
Do windy na parterze budynku wsiadło 8 osób, po czym każda z nich w sposób losowy wysiadła na jednym z pięciu pięter budynku. Jakie jest prawdopodobieństwo, że na dwóch różnych piętrach wysiadły po trzy osoby?
Punkt 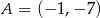 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 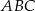 , w którym
, w którym 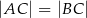 . Obie współrzędne wierzchołka
. Obie współrzędne wierzchołka 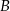 są liczbami dodatnimi. Okrąg wpisany w trójkąt
są liczbami dodatnimi. Okrąg wpisany w trójkąt 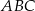 ma równanie
ma równanie 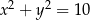 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 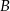 i
i 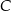 tego trójkąta.
tego trójkąta.
Rozpatrujemy wszystkie możliwe drewniane szkielety o kształcie przedstawionym na rysunku, wykonane z listewek. Każda z tych listewek ma kształt prostopadłościanu o podstawie kwadratu o boku długości  . Wymiary szkieletu zaznaczono na rysunku.
. Wymiary szkieletu zaznaczono na rysunku.
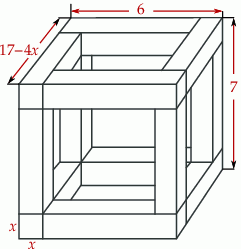
- Wyznacz objętość
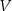 drewna potrzebnego do budowy szkieletu jako funkcję zmiennej
drewna potrzebnego do budowy szkieletu jako funkcję zmiennej  .
. - Wyznacz dziedzinę funkcji
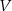 .
. - Oblicz tę wartość
 , dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja
, dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja 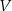 osiąga wartość największą. Oblicz tę największą objętość.
osiąga wartość największą. Oblicz tę największą objętość.

