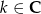/Szkoła średnia

Zadanie nr 9354475

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 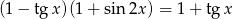(1− tg x)(1 + sin 2x) = 1 + tgx .

Rozwiązanie

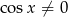Dziedzina równania to takie liczby x , że cosx ⁄= 0 (taka jest dziedzina tangensa).

Przekształcamy

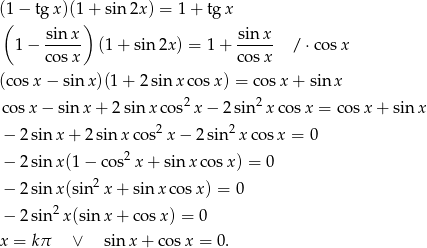
(1− tg x)(1 + sin 2x) = 1 + tgx ( sin x) sin x 1− ----- (1 + sin 2x) = 1 + ----- / ⋅cosx cos x co sx (cosx − sin x)(1 + 2sin xco sx) = co sx + sinx 2 2 cos x− sin x + 2 sin x cos x − 2 sin x cosx = cosx + sin x − 2sinx + 2 sinx cos2 x− 2sin2x cos x = 0 − 2sinx (1− cos2x + sin xcos x) = 0 2 − 2sinx (sin x + sinx cos x) = 0 − 2sin2x (sin x + cos x) = 0 x = kπ ∨ sinx + co sx = 0.

Drugie równanie rozwiążemy na dwa sposoby.

Sposób I

Korzystamy ze wzoru na sinus sumy.

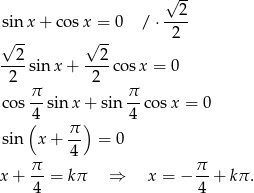
√ -- sinx + co sx = 0 / ⋅--2- √ -- √ -- 2 2 2 ----sin x + ----cos x = 0 2 π 2 π cos --sinx + sin --co sx = 0 (4 ) 4 sin x+ π- = 0 4 x+ π-= kπ ⇒ x = − π- + kπ . 4 4

Sposób II

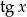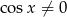Tym razem przekształcimy równanie tak, aby otrzymać tgx . Zauważmy, że z założenia cosx ⁄= 0 .

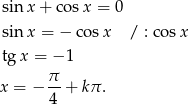
sin x+ cosx = 0 sin x = − cosx / : cos x tg x = − 1 x = − π-+ kπ . 4

 
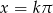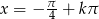Odpowiedź: x = kπ lub x = − π-+ kπ 4 , dla k ∈ C

Wersja PDF