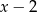/Szkoła średnia

Zadanie nr 9359395

Dodaj do ulubionych
Dodaj do rozwiązanych

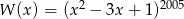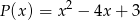Wyznacz resztę z dzielenia wielomianu 2 2005 W (x) = (x − 3x + 1) przez wielomian P(x) = x 2 − 4x + 3 .

Rozwiązanie

Zauważmy najpierw, że pierwiastkami trójmianu 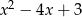2 x − 4x + 3 są liczby 1 i 3 (liczymy z 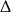Δ -y). Szukana reszta 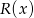R(x ) będzie wielomianem liniowym takim, że

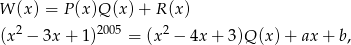
W (x) = P (x)Q (x) + R (x) 2 2005 2 (x − 3x + 1) = (x − 4x + 3)Q (x) + ax + b,

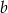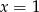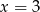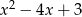dla pewnego wielomianu Q (x) . Aby wyliczyć a i b podstawmy w tej równości x = 1 i x = 3 (miejsca zerowe x2 − 4x + 3 ).

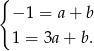
{ − 1 = a + b 1 = 3a+ b.

Odejmując od drugiego równania pierwsze (żeby skrócić 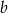b ) mamy

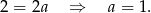
2 = 2a ⇒ a = 1.

Stąd 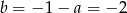b = − 1 − a = − 2 .  
Odpowiedź: x − 2

Wersja PDF