Zadanie nr 9361456
Dany jest zbiór wszystkich dwucyfrowych liczb naturalnych. Oblicz prawdopodobieństwo, że losowo wybrana z tego zbioru liczba jest podzielna przez 6 lub przez 8.
Rozwiązanie
Liczb dwucyfrowych jest 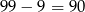 , więc
, więc
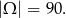
Sposób I
Liczby dwucyfrowe podzielne przez 6 to:
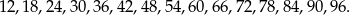
Jak widać jest ich 15.
Liczby dwucyfrowe podzielne przez 8 to:
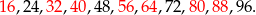
Jest ich 11, ale tylko 7 z nich nie występuje na poprzedniej licie. Prawdopodobieństwo jest więc równe
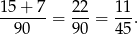
Sposób II
Liczby podzielne przez 6 to liczby
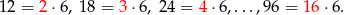
Jest ich zatem 15. Podobnie liczymy liczbę liczb podzielnych przez 8
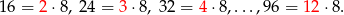
Jest ich 11.
Doszliśmy teraz do delikatnego momentu, jeżeli dodamy do siebie wyliczone liczby, to nie będzie to liczba liczb podzielnych przez 6 lub 8. Powód jest prosty: liczby które są podzielne jednocześnie przez 6 i 8 (czyli przez 24) policzyliśmy podwójnie. Musimy zatem od tej sumy odjąć liczbę liczb podzielnych przez 24. Są 4 takie liczby:
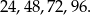
Możemy już policzyć szukane prawdopodobieństwo
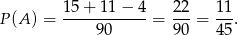
Odpowiedź: