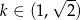/Szkoła średnia

Zadanie nr 9365081

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 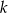k , dla których równanie 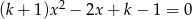2 (k + 1)x − 2x + k − 1 = 0 ma dwa różne rozwiązania należące do przedziału (0;2) .

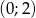Rozwiązanie

Aby równanie miało dwa pierwiastki musi być kwadratowe (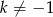k ⁄= − 1 ) oraz musi być Δ > 0 .

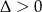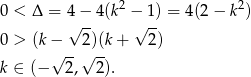
2 2 0 < Δ = 4−--4(k − 1) = 4(2 − k ) 0 > (k − √ 2)(k + √ 2) √ --√ -- k ∈ (− 2, 2).

Ponieważ wykresem funkcji 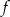f jest parabola, to podany warunek jest równoważny temu, że wierzchołek paraboli jest zawarty w podanym przedziale oraz wartości funkcji na końcach przedziału są dodatnie dla 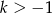k > −1 i ujemne dla k < −1 .

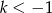Najpierw sprawdzamy wierzchołek

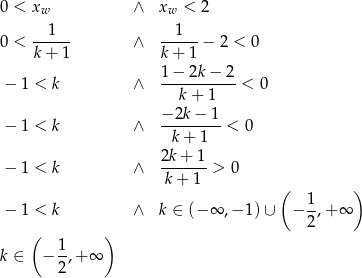
0 < xw ∧ xw < 2 1 1 0 < ------ ∧ ------− 2 < 0 k+ 1 k+ 1 1−--2k-−-2- − 1 < k ∧ k + 1 < 0 − 2k− 1 − 1 < k ∧ ---------< 0 k + 1 2k-+-1- − 1 < k ∧ k + 1 > 0 ( 1 ) − 1 < k ∧ k ∈ (− ∞ ,−1 )∪ − -,+ ∞ ( ) 2 1 k ∈ − -,+ ∞ 2

Skoro już wiemy, że 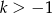k > − 1 pozostało sprawdzić kiedy 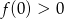f(0) > 0 i f (2) > 0 .

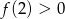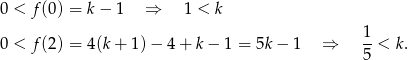
0 < f (0) = k − 1 ⇒ 1 < k 1 0 < f (2) = 4(k + 1) − 4 + k− 1 = 5k − 1 ⇒ --< k. 5

Łącząc wszystkie otrzymane warunki mamy

k ∈ (1,√ 2).

 
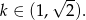
Odpowiedź: √ -- k ∈ (1, 2)

Wersja PDF