/Szkoła średnia

Zadanie nr 9366836

Dodaj do ulubionych
Dodaj do rozwiązanych

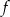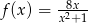Funkcja f określona jest wzorem -8x- f(x ) = x2+1 .

  • Wykaż, że funkcja 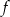f jest nieparzysta.
  • Wykaż (z definicji), że funkcja 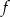f w przedziale 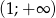(1;+ ∞ ) jest malejąca.
  • Wykaż, że funkcja 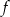f nie przyjmuje wartości większych od 4.

Rozwiązanie

  • Aby usasadnić, że funkcja jest nieparzysta musimy sprawdzić, że zachodzi równość 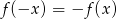f(−x ) = −f (x) . Liczymy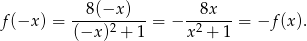
    --8(−x--)-- --8x--- f(−x ) = (−x )2 + 1 = − x2 + 1 = −f (x).
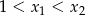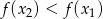  • Musimy pokazać, że jeżeli 1 < x 1 < x2 to f (x2) < f(x1) . Liczymy
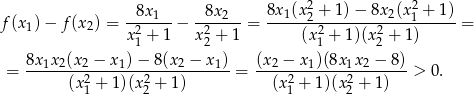
    8x1 8x2 8x 1(x22 + 1)− 8x2(x21 + 1) f(x 1)− f (x2) = --2----− -2-----= -------2--------2--------- = x 1 + 1 x2 + 1 (x1 + 1)(x 2 + 1) 8x1x2(x2-−-x1)-−-8(x2-−-x1)- (x2-−-x1)(8x1x-2 −-8-) = (x 2+ 1)(x 2+ 1 ) = (x2 + 1)(x2 + 1) > 0. 1 2 1 2

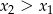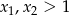    W ostatniej nierówności skorzystaliśmy z tego, że mianownik jest dodatni, x2 > x 1 i x 1,x2 > 1 .

  • Zobaczmy co dokładnie mamy wykazać
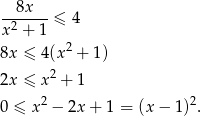
    8x -2-----≤ 4 x + 1 8x ≤ 4(x 2 + 1 ) 2 2x ≤ x + 1 0 ≤ x2 − 2x + 1 = (x− 1)2.

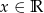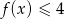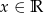    Otrzymana nierówność jest prawdziwa dla dowolnego x ∈ R , zatem f(x) ≤ 4 dla dowolnego x ∈ R .

Wersja PDF