Zadanie nr 9379163
Wykaż, że jeżeli 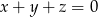 to zachodzi równość
to zachodzi równość
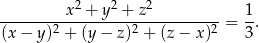
Rozwiązanie
Sposób I
Przekształcamy lewą stronę równości, którą mamy udowodnić podstawiając 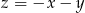 .
.
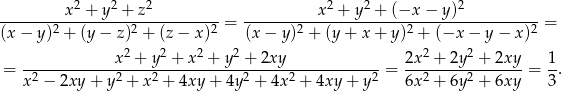
Sposób II
Korzystając ze wzoru na kwadrat sumy mamy
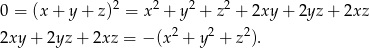
Korzystając z tej zależności mamy
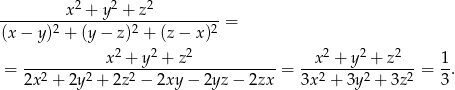
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli 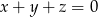 to zachodzi równość
to zachodzi równość
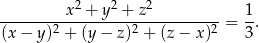
Sposób I
Przekształcamy lewą stronę równości, którą mamy udowodnić podstawiając 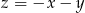 .
.
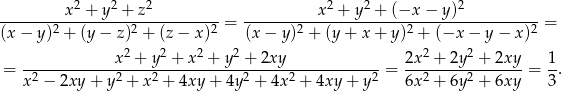
Sposób II
Korzystając ze wzoru na kwadrat sumy mamy
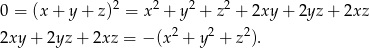
Korzystając z tej zależności mamy