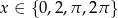Zadanie nr 9383090
Rozwiąż równanie 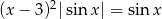 w zbiorze
w zbiorze 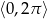 .
.
Rozwiązanie
Zauważmy najpierw, że jeżeli 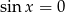 , to równanie jest spełnione, więc otrzymujemy w ten sposób 3 rozwiązania:
, to równanie jest spełnione, więc otrzymujemy w ten sposób 3 rozwiązania: 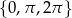 . Załóżmy dalej, że
. Załóżmy dalej, że 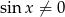 .
.
Sposób I
Rozważamy dwa przypadki (ze względu na możliwy znak sinusa).
Jeżeli 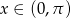 , to mamy równanie
, to mamy równanie
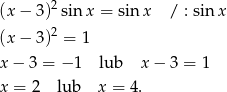
Tylko pierwsza z tych liczb spełnia warunek 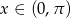 .
.
Jeżeli 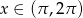 , to mamy równanie
, to mamy równanie
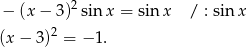
Równanie to jest oczywiście sprzeczne.
Sposób II
Zauważmy, że lewa strona danego równania jest zawsze nieujemna, więc praw strona też mus być nieujemna, czyli 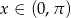 (przedział jest otwarty bo założyliśmy, że
(przedział jest otwarty bo założyliśmy, że 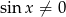 ). Równanie przyjmuje więc postać
). Równanie przyjmuje więc postać
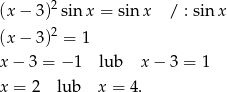
Tylko pierwsza z tych liczb spełnia warunek 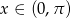 .
.
Odpowiedź: