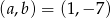/Szkoła średnia

Zadanie nr 9385624

Dodaj do ulubionych
Dodaj do rozwiązanych

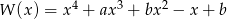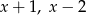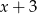Wielomian 4 3 2 W (x) = x + ax + bx − x+ b przy dzieleniu przez każdy z dwumianów: x + 1 , x − 2 i x + 3 daję tę samą resztę. Wyznacz a i b .

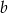Rozwiązanie

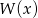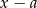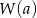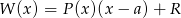Reszta z dzielenia wielomianu W (x) przez dwumian x − a to dokładnie W (a) (aby to sprawdzić wystarczy podstawić x = a w równości W (x) = P(x )(x− a)+ R ). Mamy zatem układ równań

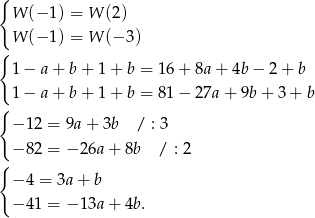
{ W (− 1) = W (2) { W (− 1) = W (− 3) 1 − a + b + 1 + b = 16 + 8a + 4b − 2 + b 1 − a + b + 1 + b = 81 − 27a + 9b + 3 + b { − 12 = 9a+ 3b / : 3 − 82 = −2 6a+ 8b / : 2 { − 4 = 3a + b − 41 = −1 3a+ 4b.

Odejmujemy od drugiego równania pierwsze pomnożone przez 4 (żeby skrócić 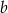b ).

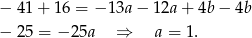
− 41 + 1 6 = − 13a − 12a + 4b − 4b − 25 = − 25a ⇒ a = 1 .

Stąd 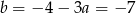b = − 4 − 3a = − 7 .  
Odpowiedź: (a,b) = (1 ,−7 )

Wersja PDF