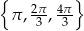/Szkoła średnia

Zadanie nr 9390695

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 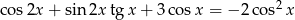2 cos 2x + sin2x tgx + 3cos x = − 2 cos x w przedziale ⟨0,2π ⟩ .

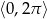Rozwiązanie

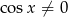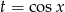Oczywiście ze względu na tangens musimy założyć, że cosx ⁄= 0 . Przekształcamy równanie tak, aby móc podstawić t = co sx .

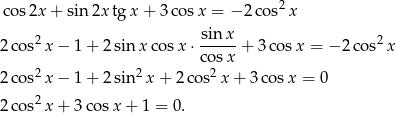
2 co s2x + sin2x tg x+ 3co sx = − 2 cos x 2 sin x 2 2co s x − 1 + 2 sin x cosx ⋅----- + 3 cosx = − 2cos x 2 2 co2sx 2co s x − 1 + 2 sin x + 2co s x + 3 cosx = 0 2co s2x + 3 cosx + 1 = 0.

Podstawiamy teraz 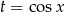t = cosx .

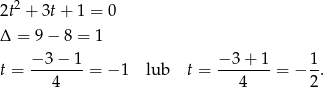
2t2 + 3t+ 1 = 0 Δ = 9− 8 = 1 − 3 − 1 − 3+ 1 1 t = ------- = − 1 lub t = -------= − --. 4 4 2

Mamy zatem

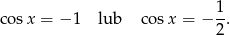
1 cos x = − 1 lub cosx = − 2.

Szkicujemy cosinusa.

PIC

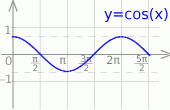
Z wykresu widać, że w danym przedziale mamy trzy rozwiązania

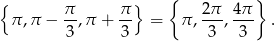
{ } { } π,π − π-,π + π- = π , 2π-, 4π . 3 3 3 3

 
Odpowiedź: { } π , 2π, 4π- 3 3

Wersja PDF