/Szkoła średnia

Zadanie nr 9397754

Dodaj do ulubionych
Dodaj do rozwiązanych

Mały Antek założył zeszyt, w którym każdego dnia zapisuje jedną liczbę. Pierwszą zapisaną przez niego liczbą było 112, a każdego następnego dnia zmniejsza wpisywaną liczbę o 7.

  • Przez ile dni Antek wpisywał do zeszytu liczby, jeżeli wśród wpisanych liczb są liczby ujemne, a suma wszystkich liczb wynosi 805.
  • Ile liczb dodatnich jest wpisanych do zeszytu?

Rozwiązanie

  • Zgodnie z treścią zadania, liczby wpisywane do zeszytu są kolejnymi wyrazami ciągu arytmetycznego o pierwszym wyrazie 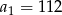a = 112 1 i różnicy 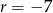r = − 7 . Po n dniach suma liczb zapisanych w zeszycie wynosi
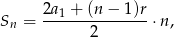
    Sn = 2a1 +-(n-−--1)r⋅ n, 2

    co daje nam równanie

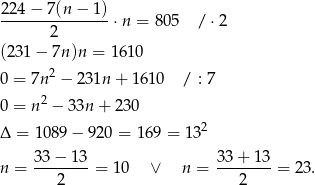
    224 − 7 (n− 1) ---------------⋅ n = 805 / ⋅2 2 (231 − 7n )n = 161 0 0 = 7n 2 − 2 31n + 1610 / : 7 0 = n 2 − 33n + 230 2 Δ = 1089 − 920 = 169 = 13 33−--13- 33+--13- n = 2 = 1 0 ∨ n = 2 = 23 .

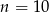    Które n wybrać? Właśnie teraz trzeba wykorzystać informację o tym, że w zeszycie są zapisane liczby ujemne. Gdyby było n = 10 , to ostatnia liczba zapisana w zeszycie byłaby dodatnia. Musi więc być n = 23 .  
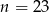    Odpowiedź: Przez 23 dni.

  • Aby sprawdzić ile liczb jest dodatnich rozwiązujemy nierówność
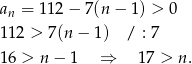
    an = 112 − 7(n − 1) > 0 1 12 > 7(n − 1) / : 7 1 6 > n − 1 ⇒ 17 > n.

    W notesie jest więc 16 dodatnich liczb.  
    Odpowiedź: Jest 16 liczb dodatnich.

Wersja PDF