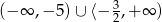Zadanie nr 9405851
Funkcja 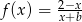 przyjmuje wartości ujemne wtedy i tylko wtedy gdy
przyjmuje wartości ujemne wtedy i tylko wtedy gdy 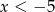 lub
lub 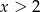 .
.
- Oblicz
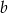 .
. - Napisz wzór funkcji
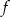 w postaci kanonicznej.
w postaci kanonicznej. - Wyznacz zbiór tych argumentów, dla których funkcja
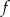 osiąga wartości nie większe niż funkcja
osiąga wartości nie większe niż funkcja 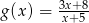 .
.
Rozwiązanie
- Funkcja
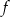 jest ujemna dokładnie w tych samych przedziałach co trójmian
jest ujemna dokładnie w tych samych przedziałach co trójmian 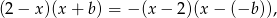
który jest ujemny poza przedziałem o końcach
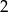 i
i 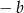 . Zatem musi być
. Zatem musi być 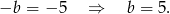
Odpowiedź: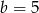
- Przekształcamy
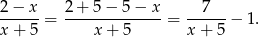
Odpowiedź: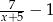
- Mamy nierówność
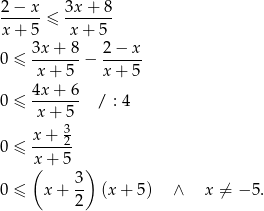
Rozwiązaniem tej nierówności jest zbiór
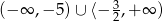 .
.
Odpowiedź: