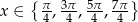/Szkoła średnia

Zadanie nr 9405978

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 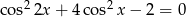2 2 cos 2x + 4co s x − 2 = 0 w zbiorze ⟨0,2π ⟩ .

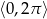Rozwiązanie

Korzystamy ze wzoru

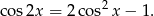
2 co s2x = 2cos x− 1.

Sposób I

Przekształcamy równanie.

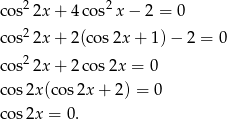
cos22x + 4 cos2x − 2 = 0 2 cos 2x + 2 (cos2x + 1) − 2 = 0 cos22x + 2 cos 2x = 0 cos2x (cos2x + 2 ) = 0 cos2x = 0.

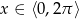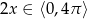Teraz trzeba odrobinę uważać, bo wprawdzie x ∈ ⟨0,2π ⟩ , ale 2x ∈ ⟨0,4π ⟩ . Szkicujemy cosinusa.

PIC

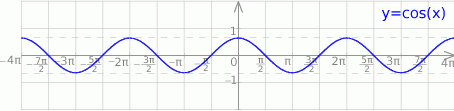
Z obrazka odczytujemy, że

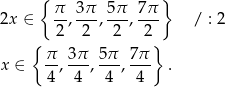
{ } π- 3π- 5π- 7-π 2x ∈ 2 , 2 , 2 , 2 / : 2 { } x ∈ π-, 3π-, 5π-, 7π . 4 4 4 4

Sposób II

Tym razem przekształcamy równanie pozbywając się 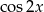cos2x .

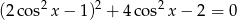
(2cos2 x− 1)2 + 4cos2 x− 2 = 0

Zanim przekształcimy to dalej, podstawmy 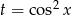t = co s2 x .

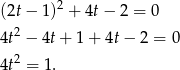
2 (2t− 1 ) + 4t − 2 = 0 4t2 − 4t + 1 + 4t− 2 = 0 4t2 = 1.

Ponieważ 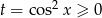t = co s2x ≥ 0 , mamy stąd 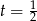t = 1 2 , czyli

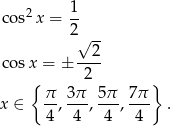
1 cos2x = -- 2√ -- --2- cosx = ± 2 { π 3 π 5π 7π } x ∈ --,--- ,---,--- . 4 4 4 4

 
Odpowiedź: { } x ∈ π4-, 34π, 5π4-, 74π

Wersja PDF