/Szkoła średnia

Zadanie nr 9408222

Dodaj do ulubionych
Dodaj do rozwiązanych

Na trzech loteriach kupiono po jednym losie. Prawdopodobieństwo wygrania na pierwszej loterii wynosi 50%, na drugiej 60%, a na trzeciej 70%. Jakie jest prawdopodobieństwo:

  • wygrania na trzech loteriach;
  • niewygrania na żadnej;
  • wygrania przynajmniej na jednej loterii.

Rozwiązanie

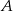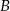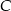Oznaczmy prawdopodobieństwa wygrania na kolejnych loteriach przez A , B i C odpowiednio. Mamy zatem

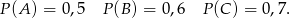
P (A) = 0,5 P (B) = 0,6 P(C ) = 0,7.

Ponieważ są to trzy niezależne loterie, to

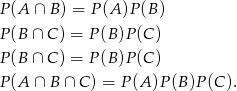
P(A ∩ B) = P (A )P (B) P(B ∩ C ) = P(B )P(C ) P(B ∩ C ) = P(B )P(C ) P(A ∩ B ∩ C) = P (A )P(B )P(C ).

Jeżeli ktoś w to nie dowierza, to może sobie te wzory wyprowadzić, oznaczając liczby wszystkich losów w każdej z loterii i wyliczając liczbę zdarzeń sprzyjających dwóm (lub trzem) loteriom na raz.

  • Jak zauważyliśmy powyżej
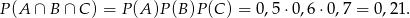
    P (A ∩ B ∩ C ) = P (A)P (B)P (C) = 0,5⋅0 ,6⋅0,7 = 0,21.

     
    Odpowiedź: 0,21

  • Interesuje nas zdarzenie 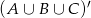(A ∪ B ∪ C )′ . Liczymy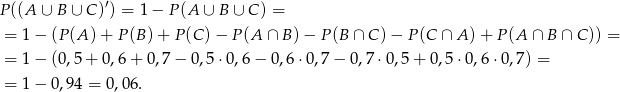
    P ((A ∪ B ∪ C )′) = 1− P(A ∪ B ∪ C ) = = 1− (P(A )+ P(B )+ P (C) − P (A ∩ B )− P (B ∩ C) − P (C ∩ A )+ P (A ∩ B ∩ C )) = = 1− (0,5+ 0,6+ 0,7− 0,5⋅0 ,6− 0,6⋅0,7 − 0 ,7 ⋅0,5 + 0,5 ⋅0,6 ⋅0,7) � = 1− 0,94 = 0,06.

    Wzór na 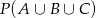P(A ∪ B ∪ C ) , z którego korzystaliśmy, najłatwiej sobie wyprowadzić rysując diagram Venna.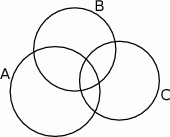

    PIC

    Mogliśmy też to policzyć trochę prościej, korzystając z praw d’Morgana

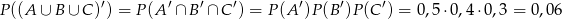
    P ((A ∪ B ∪ C)′) = P (A′∩ B ′∩ C′) = P (A′)P (B′)P(C ′) = 0 ,5⋅0,4 ⋅0,3 = 0,06

     
    Odpowiedź: 0,06

  • Interesujące nas zdarzenie to dokładnie zdarzenie przeciwne do zdarzenia z poprzedniego podpunktu, zatem
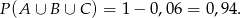
    P (A ∪ B ∪ C) = 1− 0,06 = 0,94 .

     
    Odpowiedź: 0,94

Wersja PDF