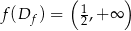/Szkoła średnia

Zadanie nr 9411924

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz dziedzinę i zbiór wartości funkcji

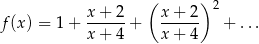
( )2 f(x ) = 1+ x-+-2-+ x-+-2- + ... x + 4 x + 4

Naszkicuj wykres funkcji 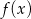f(x) .

Rozwiązanie

Wzór definiujący funkcję 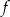f , to suma szeregu geometrycznego o ilorazie 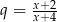q = xx++24- . Sprawdźmy najpierw, kiedy szereg ten jest zbieżny, tzn. kiedy |q| < 1 .

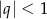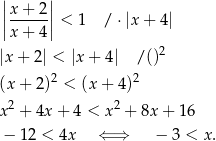
| | ||x-+--2||< 1 / ⋅|x + 4| |x + 4| 2 |x+ 2| < |x+ 4| /() (x + 2)2 < (x + 4)2 x2 + 4x + 4 < x2 + 8x+ 16 − 12 < 4x ⇐ ⇒ − 3 < x.

Oczywiście musimy też mieć 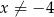x ⁄= −4 (ze względu na mianownik), ale przy otrzymanym warunku: 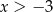x > − 3 jest to spełnione automatycznie.

Wiem już kiedy szereg jest zbieżny, to obliczmy jego sumę.

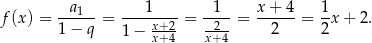
f (x) = --a1--= ---1----= --1- = x+--4-= 1-x+ 2. 1 − q 1 − xx++-24 x+24 2 2

Jest to więc fragment rosnącej funkcji liniowej.

PIC

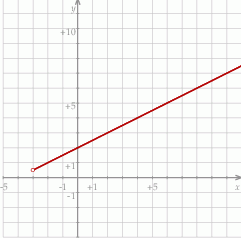
Zbiorem wartości tej funkcji jest przedział

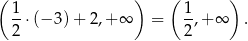
( ) ( ) 1⋅ (− 3)+ 2 ,+∞ = 1-,+ ∞ . 2 2

 
Odpowiedź: 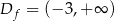Df = (− 3,+ ∞ ) , ( ) f (Df) = 1,+ ∞ 2

Wersja PDF