/Szkoła średnia

Zadanie nr 9420931

Dodaj do ulubionych
Dodaj do rozwiązanych

Określ dziedzinę i zbiór wartości funkcji 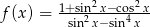1+sin2-x−-cos2x- f(x ) = sin2x− sin4x .

Rozwiązanie

Rozpocznijmy od wyznaczenia dziedziny funkcji

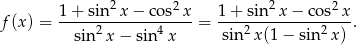
2 2 2 2 f(x) = 1+--sin--x-−-cos-x--= 1-+-sin--x−--cos-x-. sin 2x − sin4x sin2x(1 − sin2 x)

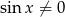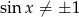Ze względu na mianownik musi być sinx ⁄= 0 i sin x ⁄= ± 1 . Mamy stąd

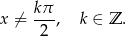
kπ- x ⁄= 2 , k ∈ Z .

Zanim wyznaczymy zbiór wartości, przekształćmy wzór funkcji 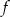f .

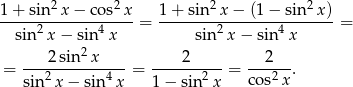
1-+-sin2x-−-cos2-x- 1+--sin-2x-−-(1-−-sin2x)- sin2x − sin4 x = sin 2x − sin4x = 2 = ----2sin-x---- = ----2-----= --2---. sin2x − sin4 x 1− sin 2x cos2x

Ponieważ 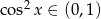cos2x ∈ (0 ,1 ) (ze względu na dziedzinę), zbiorem wartości funkcji 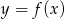y = f(x) jest przedział (2,+ ∞ ) .  
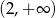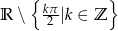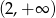Odpowiedź: Dziedzina: { } R ∖ kπ2-|k ∈ Z , zbiór wartości: (2,+ ∞ ) .

Wersja PDF