/Szkoła średnia

Zadanie nr 9428965

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 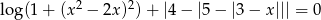2 2 log(1 + (x − 2x ) )+ |4 − |5− |3 − x ||| = 0 .

Rozwiązanie

Zauważmy, że 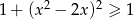2 2 1+ (x − 2x ) ≥ 1 , czyli

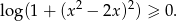
2 2 log(1 + (x − 2x) ) ≥ 0 .

Nieujemny jest także drugi składnik lewej strony równania, zatem lewa strona może być równa 0 tylko wtedy, gdy oba składniki są równe 0. Patrząc na pierwszy składnik, mamy więc

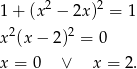
1+ (x 2 − 2x )2 = 1 2 2 x (x− 2) = 0 x = 0 ∨ x = 2.

Zauważmy teraz, że nie musimy rozwiązywać równania

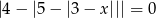
|4− |5 − |3 − x||| = 0

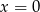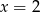wystarczy tylko sprawdzić, która z liczb x = 0 i x = 2 je spełnia. Liczymy

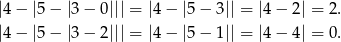
|4 − |5− |3− 0 ||| = |4− |5 − 3|| = |4− 2| = 2. |4 − |5− |3− 2 ||| = |4− |5 − 1|| = |4− 4| = 0.

Zatem jedyne rozwiązanie danego równania to 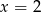x = 2 .  
Odpowiedź: x = 2

Wersja PDF