/Szkoła średnia

Zadanie nr 9435632

Dodaj do ulubionych
Dodaj do rozwiązanych

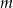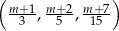Wykaż, że dla każdego m ciąg (m-+1 m+2- m+7-) 3 , 5 , 15 jest arytmetyczny.

Rozwiązanie

Sposób I

Trzy liczby 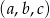(a,b,c) są kolejnymi wyrazami ciągu arytmetycznego wtedy i tylko wtedy, gdy 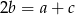2b = a + c . Sprawdźmy czy tak jest w naszej sytuacji.

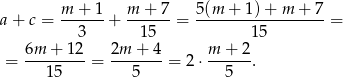
m + 1 m + 7 5(m + 1) + m + 7 a + c = ------+ ------= ------------------ = 3 15 15 = 6m-+--12-= 2m-+-4-= 2⋅ m-+--2. 15 5 5

Zatem istotnie podane liczby tworzą ciąg arytmetyczny.

Sposób II

Wystarczy sprawdzić, że różnice między kolejnymi wyrazami są równe. Liczymy

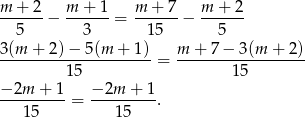
m + 2 m + 1 m + 7 m + 2 ------ − ------ = ------− ------ 5 3 15 5 3(m--+-2)−--5(m-+--1) m--+-7-−-3(m-+--2) 15 = 15 − 2m + 1 − 2m + 1 --------- = ---------. 1 5 15

Otrzymana równość jest oczywiście prawdziwa, co dowodzi, że dane liczby tworzą ciąg arytmetyczny.

Wersja PDF