Zadanie nr 9458239
W trójkącie 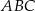 dane są wierzchołki
dane są wierzchołki 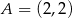 ,
, 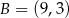 ,
, 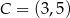 . Trójkąt
. Trójkąt 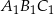 jest obrazem trójkąta
jest obrazem trójkąta 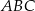 w jednokładności o środku
w jednokładności o środku 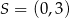 i skali
i skali 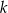 . Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie
. Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie 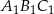 ma długość
ma długość 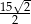 . Skala jednokładności
. Skala jednokładności 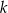 wynosi
wynosi
A) 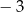 B)
B) 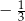 C)
C) 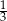 D) 3
D) 3
Rozwiązanie
Szkicujemy opisaną sytuację.
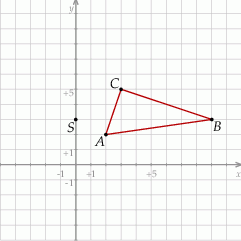
Nawet ze szkicowego rysunku powinno się rzucać w oczy, że trójkąt 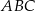 jest prostokątny. Sprawdźmy, czy rzeczywiście tak jest.
jest prostokątny. Sprawdźmy, czy rzeczywiście tak jest.
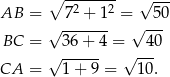
Zatem rzeczywiście 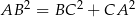 i trójkąt
i trójkąt  jest prostokątny. W takim razie promień
jest prostokątny. W takim razie promień  okręgu opisanego na tym trójkącie jest równy
okręgu opisanego na tym trójkącie jest równy
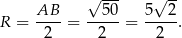
Wiemy, że promień okręgu opisanego na trójkącie 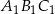 jest 3 razy dłuższy, więc
jest 3 razy dłuższy, więc 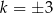 . Gdyby jednak
. Gdyby jednak 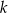 było dodatnie, to oba trójkąty leżałyby po tej samej stronie osi
było dodatnie, to oba trójkąty leżałyby po tej samej stronie osi 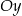 . Zatem
. Zatem 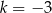 .
.
Odpowiedź: A

