/Szkoła średnia

Zadanie nr 9473196

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 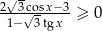2√-3cosx−3 1− √3tgx ≥ 0 w przedziale ⟨π,2 π⟩ .

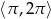Rozwiązanie

Przekształćmy odrobinę daną nierówność tak, żeby było widać kiedy zeruje się licznik, a kiedy mianownik.

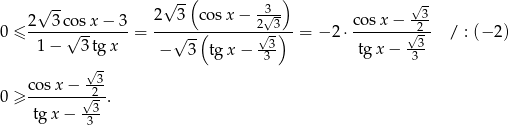
√ -- √ --( ) √ - 2 3 cosx − 3 2 3 co sx − 23√-3 co sx − --3 0 ≤ -----√--------= ---√--(-------√--)- = −2 ⋅--------√2- / : (− 2) 1 − 3 tg x − 3 tg x − -33 tgx − 33- √- cos x− -3- 0 ≥ -------√-2-. tg x − -33

Mianownik musi oczywiście być niezerowy, co w podanym przedziale oznacza, że 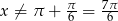π 7π x ⁄= π + 6-= -6- .

PIC

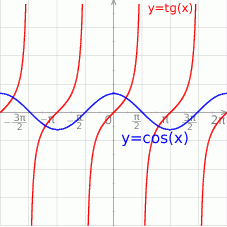
Ponadto ze względu na dziedzinę tangensa musi być 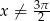x ⁄= 32π- .

Dana nierówność będzie spełniona gdy licznik i mianownik różnią się znakiem lub gdy licznik jest równy 0. Mam więc

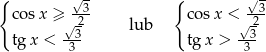
{ √- { √- co sx ≥ -3- co sx < -3- √2 lub √ 2 tg x < 33- tg x > -33

Rozwiązaniem pierwszego układu nierówności jest przedział

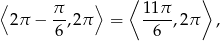
⟨ ⟩ ⟨ ⟩ π- 1-1π 2π − 6 ,2π = 6 ,2π ,

a drugiego przedział

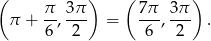
( ) ( ) π- 3π- 7π- 3π- π + 6 , 2 = 6 , 2 .

Rozwiązaniem danej nierówności jest więc zbiór

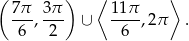
( ) ⟨ ⟩ 7π 3π 1 1π ---,--- ∪ ---- ,2π . 6 2 6

 
Odpowiedź: 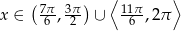( 7π 3π ) ⟨ 11π ⟩ x ∈ 6-,-2- ∪ -6-,2π .

Wersja PDF