/Szkoła średnia

Zadanie nr 9490789

Dodaj do ulubionych
Dodaj do rozwiązanych

Cenę sukienki obniżano dwukrotnie, za każdym razem o ten sam procent. W wyniku tych obniżek cena sukienki ze 100 zł spadła do 96,04 zł. Oblicz, o ile procent za każdym razem obniżano cenę sukienki.

Rozwiązanie

Sposób I

Oznaczmy przez 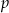p procent o jaki obniżano cenę sukienki, oraz niech 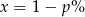x = 1− p% . W takim razie cena sukienki po pierwszej obniżce wynosiła

100⋅ x,

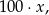
a po drugiej

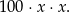
100 ⋅x ⋅x.

Mamy zatem równanie

2 100x = 96,04 / : 100 x2 = 0,9 604 x = − 0,9 8 lub x = 0,98.

Ujemne rozwiązanie odrzucamy i mamy 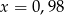x = 0,98 . Stąd

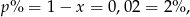
p% = 1 − x = 0,02 = 2% ,

czyli 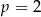p = 2 .

Sposób II

Oznaczmy przez 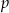p procent o jaki obniżano cenę sukienki. Po pierwszej obniżce cena sukienki wynosiła

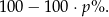
1 00− 100 ⋅p% .

Natomiast po drugiej cena była równa

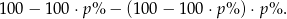
1 00− 100⋅ p% − (100 − 100 ⋅p% ) ⋅p% .

Stąd otrzymujemy równanie

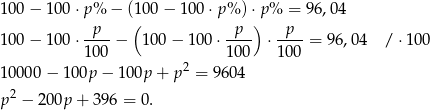
100− 100 ⋅p% − (100 − 100 ⋅p% ) ⋅p% = 96 ,04 ( ) 100− 100 ⋅-p--− 100 − 100 ⋅-p-- ⋅-p-- = 96,0 4 / ⋅100 100 1 00 10 0 10000 − 100p − 100p + p2 = 9604 2 p − 200p + 396 = 0.

Liczymy wyróżnik

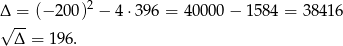
2 Δ√ -= (− 200) − 4 ⋅396 = 40000 − 158 4 = 38416 Δ = 196 .

Obliczamy 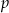p

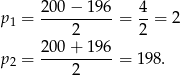
20-0−--196 4- p1 = 2 = 2 = 2 20 0+ 196 p2 = ---------- = 1 98. 2

Odrzucamy liczbę 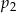p2 ponieważ obniżenie o 198% oznaczałoby, że sukienka po pierwszej obniżce miałaby ujemną cenę. Zatem 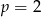p = 2 , czyli cenę sukienki obniżano o 2%.  
Odpowiedź: O 2%.

Wersja PDF