/Szkoła średnia

Zadanie nr 9491504

Dodaj do ulubionych
Dodaj do rozwiązanych

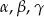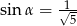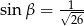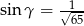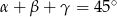Wykaż, że jeżeli α,β ,γ są kątami ostrymi i -1- sin α = √ 5 , -1-- sin β = √26 , sin γ = √1-- 65 to α+ β+ γ = 4 5∘ .

Rozwiązanie

Zauważmy, że z podanych sinusów wynika, że 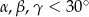∘ α,β,γ < 30 , więc 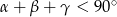α + β + γ < 90∘ . Wystarczy zatem wykazać, że 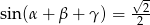√ - sin(α + β + γ ) = --2 2 . Zrobimy to korzystając ze wzorów na sinus/cosinus sumy, ale najpierw obliczmy cosinusy danych kątów (korzystamy z tego, że kąty są ostre!).

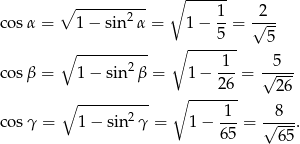
∘ ---------- ∘ ------ cosα = 1 − sin2α = 1 − 1-= √2-- 5 5 ∘ ---------- ∘ -----1- 5 cosβ = 1 − sin2β = 1 − --- = √---- 2 6 2 6 ∘ ---------- ∘ -----1- 8 cosγ = 1 − sin2γ = 1 − ---= √---. 65 65

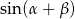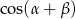Liczymy najpierw sin(α + β) i cos(α + β) .

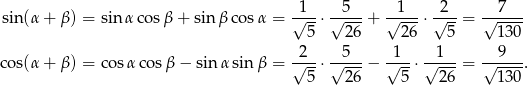
sin(α + β) = sin α cosβ + sin βco sα = √1--⋅√-5--+ √1---⋅√2--= √-7--- 5 26 26 5 130 2 5 1 1 9 cos(α + β) = cosα cos β− sin α sin β = √---⋅√----− √--⋅ √----= √----. 5 26 5 26 130

Liczymy teraz 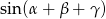sin(α + β + γ ) .

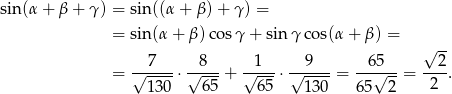
sin(α + β + γ ) = sin((α + β) + γ) = = sin(α + β) cosγ + sin γ cos(α + β) = √ -- = √-7---⋅ √8---+ √-1--⋅ √-9---= -65√---= --2. 130 65 65 130 65 2 2

Zatem rzeczywiście 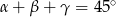α+ β+ γ = 4 5∘ .

Wersja PDF