Zadanie nr 9492318
Funkcja kwadratowa 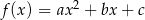 , spełnia warunek
, spełnia warunek 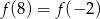 . Wykaż, że dla dowolnej liczby rzeczywistej
. Wykaż, że dla dowolnej liczby rzeczywistej  , spełniony jest warunek
, spełniony jest warunek 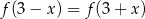 .
.
Rozwiązanie
Sposób I
Rozszyfrujmy najpierw warunek 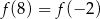 .
.
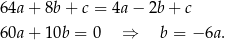
W takim razie 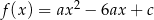 i
i
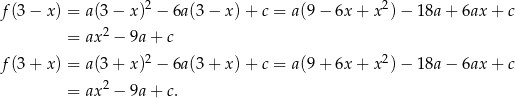
Zatem rzeczywiście 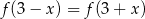 .
.
Sposób II
Warunek 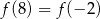 oznacza, że osią symetrii paraboli będącej wykresem funkcji
oznacza, że osią symetrii paraboli będącej wykresem funkcji 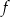 jest prosta
jest prosta 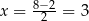 .
.
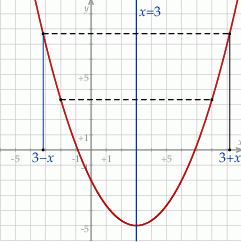
Teraz wystarczy zauważyć, że punkty tego wykresu o pierwszych współrzędnych równych 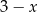 i
i 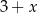 odpowiednio też są położone symetrycznie względem prostej
odpowiednio też są położone symetrycznie względem prostej 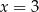 , bo
, bo
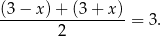
W takim razie rzeczywiście 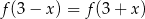 .
.

