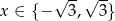/Szkoła średnia

Zadanie nr 9503393

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 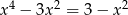4 2 2 x − 3x = 3 − x .

Rozwiązanie

Sposób I

Jeżeli się przyjrzymy to widać, że po obu stronach równania można wyłączyć 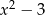x 2 − 3 przed nawias.

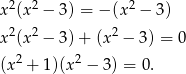
2 2 2 x (x − 3 ) = − (x − 3) x2(x 2 − 3 )+ (x 2 − 3) = 0 (x2 + 1)(x 2 − 3) = 0.

Wyrażenie w pierwszym nawiasie jest zawsze dodatnie, więc pozostaje równanie

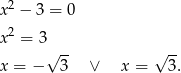
x2 − 3 = 0 2 x = 3 √ -- √ -- x = − 3 ∨ x = 3.

Sposób II

Jeżeli zapiszemy dane równanie w postaci

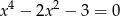
4 2 x − 2x − 3 = 0

to widać, że mamy do czynienia z równaniem dwukwadratowym i możemy podstawić 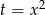2 t = x .

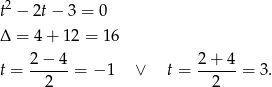
2 t − 2t− 3 = 0 Δ = 4 + 12 = 1 6 t = 2−-4-= − 1 ∨ t = 2-+-4-= 3. 2 2

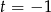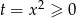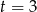t = − 1 nie daje żadnych rozwiązań (bo 2 t = x ≥ 0 ), a t = 3 daje dwa rozwiązania √ -- x = ± 3 .  
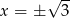Odpowiedź: √ -- √ -- x ∈ { − 3 , 3}

Wersja PDF